定量销售预测主要是根据产品销售的实际历史资料，运用特定的方法确定销售中有关因素之间的数量关系及其变化规律，然后据以测算未来的产品销售情况。定量销售预测通常在具有系统、完备的历史观察数据，或者影响未来的销售量发生变动的有关因素可以量化的情况下采用。

定量销售预测常用的方法有移动平均法、加权移动平均法、趋势平均法、指数平滑法及直线回归分析法等。

1.移动平均法

移动平均法是指在掌握n 期销售量的基础上，按照事先确定的期数逐期分段计算m 期算术平均数，并以最后一个m 期平均数作为未来n＋1 期预测销售量的一种方法。所谓“移动”是指预测值随着时间的不断推移，计算的平均值也在不断向后顺延。此法假定预测值主要受最近m 期销售业务量的影响。此法的计算公式是

【例5-1】某企业生产一种产品，2017年1～12月销量资料如表5-1所示。要求按移动平均法预测2018年1月份的销售量（假定m＝5）。

表5-1　销售资料

解：依式（5-1），利用最后5 期销售量资料，得

1月份预测销售量＝（34＋34＋32＋35＋36）÷5＝34.2（吨）

答：1月份预测销售量为34.2 吨。

但统计学家认为这样计算的平均值只反映预测期前期的销售水平，还应在此基础上，按趋势值进行修正。趋势值b 的计算公式为

修正的移动平均法按以下公式进行预测：

【例5-2】仍按表5-1所示资料，要求用修正的移动平均法预测来年1月份的销售量（假定m＝5）。

解：因为【例5-1】中的最后移动期的平均值为34.2，上一个移动期的平均值＝（31＋34＋34＋32＋35）÷5＝33.2，所以b＝34.2-33.2＝1。

1月份预测销售量＝34.2＋1＝35.2（吨）

答：按修正的移动平均法计算的来年1月份预测销售量为35.2 吨。

移动平均法考虑到远近期销售量对预测量影响程度不同，但只考虑n 期数据中的最后m期资料，缺乏代表性。此法适于销售量略有波动的产品销售量预测。

2.加权移动平均法

加权移动平均法是根据过去若干期的销售量（或销售额）按其距计划期的远近分别进行加权，计算其加权平均数，并据以作为计划期的销售预测数的一种方法。计算公式为

式中，w 代表权数；x 代表销售量（或销售额）。

【例5-3】仍按表5-1所示资料，要求采用加权移动平均法预测来年1月份预测销售量。

解：按照距预测期的远近不同，令权数w 分别为1，2，3，根据计算公式预测来年1月份预测销售量如下：

为简化计算，也可令∑w＝1（如令w1为0.2，w2为0.3，w3为0.5），则计划期销售预测数的公式改写为

但统计学家认为这一方法只代表计划期前一期的实际销售水平，为了反映近期的销售发展趋势，应在上述公式的基础上再加上每月的变动趋势值b，才能作为计划期销售预测值，那么其计算公式应为

上式中，

b＝（本季度每月平均实际销售额-上季度每月平均实际销售额）÷3.

仍按表5-1所示资料为例，按加权移动平均法预测来年1月份预测销售量。

因为：

三季度每月平均销售量＝（31＋34＋34）÷3＝33（吨）

四季度每月平均销售量＝（32＋35＋36）÷3≈34.33（吨）

所以：变动趋势值b＝（34.33-33）÷3＝0.44

若令w1为0.2，w2为0.3，w3为0.5，∑w＝1。则

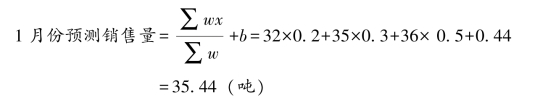
可见，这种方法考虑到近期的销售发展趋势，同时又根据时期的远近分别加权，从而消除了各个月份销售差异的平均化，故其预测结果比较接近计划期的实际情况。

3.趋势平均法

趋势平均法是指在按移动平均法计算若干期时间序列移动平均值的基础上，进一步计算趋势值的移动平均值，进而利用特定基期销售量移动平均值和趋势值移动平均值来预测未来销售量的一种方法。计算公式为

式中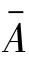，为五期平均值；n 为距离预测时间的期数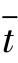；为趋势平均值。

【例5-4】仍按表5-1所示资料，要求采用趋势平均法预测来年1月份预测销售量。

解：依题意计算各期销售量移动平均值、趋势值和趋势值移动平均值，其结果如表5-2所示。(www.daowen.com)

表5-2　趋势平均法计算表

该企业计划期1月份的销售预测值计算如下：

34.2 是最后一个五期平均数；3 是最后一个五期平均数所在月份距预测期的月份数；0.47 是最后一个三期趋势平均数。

趋势平均法的优点在于既考虑了销售量的移动平均数，又考虑了趋势值的移动平均数，其缺点是过于复杂。

4.指数平滑法

指数平滑法是指在综合考虑有关前期预测销售量和实际销售量信息的基础上，利用事先确定的平滑指数预测未来销售量的一种方法。其计算公式是

a 表示平滑指数，这是一个经验数据，其取值范围通常在0.3～0.7。平滑指数具有修匀实际数所包含的偶然因素对预测值的影响的作用，平滑指数取值越大，则近期实际数对预测结果的影响就越大；平滑指数取值越小，则近期实际数对预测结果的影响就越小。因此，进行近期预测或销量波动较大时的预测，应采用较大的平滑指数；进行长期预测或销量波动较小时的预测，可采用较小的平滑指数。

【例5-5】2017年12月，计算的预测销售量为32 吨，当月实际销售量为33 吨，设平滑指数a＝0.3。要求用平滑指数法预测2018年1月份的销售量。

解：依题意按式（5-6），可求得

2018年1月份的销售量＝0.3×33＋（1-0.3）×32＝32.3（吨）

答：2018年1月份按平滑指数法预测的销售量约为32.3 吨。

从平滑指数法的预测公式和实例可看出，该法的实质是在已知前期预测销售量和实际销售量的基础上，分别以平滑指数和（1-平滑指数）为权数的一种特殊加权平均法。该法比较灵活，适用范围较广，但在选择平滑指数时，存在一定的随意性。

5.直线回归分析法

直线回归分析法就是根据过去各期的实际销售额，求出一条趋势变动直线，并使此直线上各点到实际值的对应点之间的距离为最小。用这条回归直线预测未来销售情况的方法叫直线回归分析法。

运用直线回归分析法进行预测时，首先应将过去一定时期的历史资料按时间序列在坐标上作图，如果能大致形成一条直线，则说明这个变量是时间的函数，它们之间基本上存在着线性联系，然后再建立直线回归方程

式中，x 代表自变量；y 代表因变量；a 代表纵轴截距；b 代表直线斜率。

式中a、b 的值计算公式是

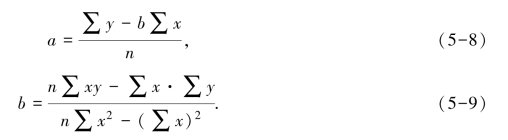
采用直线回归分析法进行销售预测时，因为x 代表时间的间隔期，间隔时间是相等的，所以可以简化计算，设法使∑x＝0。若实际观测期为奇数，则取x 的间隔期为1，将x＝0置于所有观测期的中间，其余上下均以1 递增或递减；若实际观测期为偶数，则取x 的间隔期为2，将x＝＋1 与x＝-1 置于所有观测期的中间两期，其余上下均以2 递增或递减。因为∑x＝0，所以a 与b 的计算公式便简化为

【例5-6】某企业2012—2017年某产品的实际销售额如表5-3所示。

表5-3　某产品销售情况

根据以上资料，采用直线回归分析法预测2018年某产品的销售额。

（1）时间序列期数为偶数。

根据已知的资料进行加工整理，如表5-4所示。

表5-4　直线回归分析表

将表中最后一行资料代入a、b 的计算公式

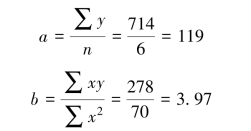
故回归直线方程为

y＝119＋3.97x.

2018年的x 值为7（5＋2），则

2018年销售预测值y＝119＋3.97×7＝146.79（万元）

（2）时间序列期数为奇数。

将2013—2017年实际销售额资料进行加工整理，如表5-5所示。

表5-5　直线回归分析表

将表中最后一行资料代入a、b 的计算公式

故回归直线为

y＝122.8＋8.2x.

2018年的x 值为3（2＋1），则

2018年销售预测值＝122.8＋8.2×3＝147.4（万元）