常用的成本性态分析方法有技术测定法、直接分析法和历史资料分析法。这些方法往往既可以应用于单步骤分析程序，又可以应用于多步骤分析程序。

1.技术测定法

技术测定法又称工程技术法，是指利用经济工程项目财务评价技术方法所测定的企业正常生产过程中投入与产出的关系，分析确定在实际业务量基础上其固定成本和变动成本水平，并揭示其变动规律的一种方法，适用于投入量与产出量关系比较稳定的新企业及其主要成本的测算。此法应用起来比较复杂，需要花费较多的时间和费用。

2.直接分析法

直接分析法是指在掌握有关项目成本性态的基础上，在成本发生的当时对每项成本的具体内容进行直接分析，使其分别归属于固定成本或变动成本的一种方法。此法在很大程度上属于定性分析，凡具有一定会计知识和业务能力的人都能掌握，属于典型的单步骤分析程序，适用于管理会计基础工作开展较好的企业。但由于此法要求掌握大量第一手资料，实际分析的工作量太大，因此，不适于规模较大企业的成本性态分析。

3.历史资料分析法

历史资料分析法是指在占有若干期相关的成本（y）和业务量（x）历史资料的基础上，运用一定数学方法对其进行数据处理，从而确定常数a 和b 的数值，以完成成本性态分析任务的一种定量分析的方法。这里的成本y 是分析对象，既可以代表总成本，又可以代表某项混合成本（这主要取决于选择哪一种成本分析程序）。由于分析对象y 的不同，a 可以分别代表固定成本总额或混合成本中的固定部分；b 则可分别表示单位变动成本或混合成本中变动部分的单位额。

该法要求企业资料齐全，成本数据与业务量的资料要同期配套，具备相关性，并以企业的历史成本与未来成本具有相似性为前提。因此，此法适用于生产条件较为稳定、成本水平波动不大以及有关历史资料比较完备的老企业。

历史资料分析法包括高低点法、散布图法、一元直线回归法和财务分析法四种具体应用形式。

1）高低点法

高低点法又叫两点法，是指通过观察一定相关范围内的各期业务量与相关成本所构成的所有坐标点，从中选出高低两点坐标，并据此来推算固定成本总额（或混合成本中的固定部分）a 和单位变动成本（或混合成本中变动部分的单位额）b 的一种成本性态分析方法。此法的基本原理是解析几何中的两点法。

高低点法的具体步骤是：

①从由各期业务量与相关成本所构成的所有坐标点中，找出由最高业务量及同期成本组成的高点坐标（x1，y1）和由最低业务量及同期成本组成的低点坐标（x2，y2）。

②将高低点坐标值代入下式，计算单位变动成本b。

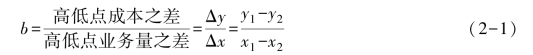
③将低点或高点坐标值和b 值代入下式，计算固定成本a。

或

④将a、b 值代入下式，写出一般成本性态模型：

【例2-5】已知A 企业2015年上半年B 产品产量与某项混合成本的资料如表2-3所示，要求用高低点法进行成本性态分析。

表2-3　A 企业2015年上半年资料

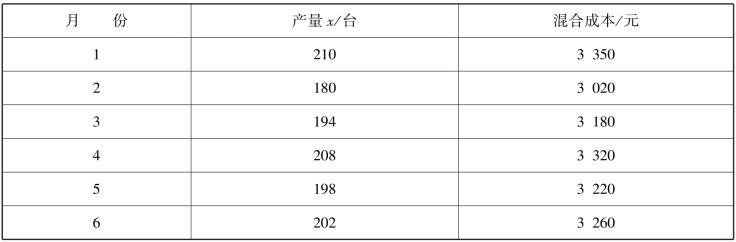
解：根据上述资料可断定，高点坐标为（210，3 350）；低点坐标为（180，3 020）。

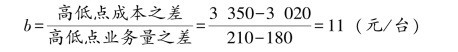
将低点或高点坐标值和b＝11 代入下式，计算固定成本a。

a＝3 020-11×180＝1 040＝3 350-11×210＝1 040（元）

答：该项混合成本的性态模型为y＝1 040＋11x，其中固定部分为1 040 元，变动部分为11x。

2）散布图法

散布图法是指将若干期业务量和成本的历史数据标注在坐标纸上，通过目测画一条尽可能接近所有坐标点的直线，并据此来推算固定成本（或混合成本中的固定部分）a 和单位变动成本（或混合成本中变动部分的单位额）b 的一种成本性态分析方法。此法又称目测画线法。

散布图法的具体步骤是：

①建立平面坐标系，以纵轴y 代表成本，以横轴x 代表业务量。

②将各期业务量与相应成本的历史资料作为点的坐标标注在平面直角坐标图上。

③目测画一条直线，使其尽可能通过或接近所有坐标点。

④在纵轴上读出该直线的截距值，即固定成本总额a。

⑤在直线上任取一点P，假设其坐标值为（xi，yi）。将它们代入下式计算单位变动成本b。

(www.daowen.com)

⑥将a、b 值代入下式，写出一般成本性态模型：

y＝a＋bx

【例2-6】已知B 企业2016年上半年甲产品产量与某项混合成本的资料如表2-4所示，要求用散布图法进行成本性态分析。

表2-4　B 企业2016年上半年资料

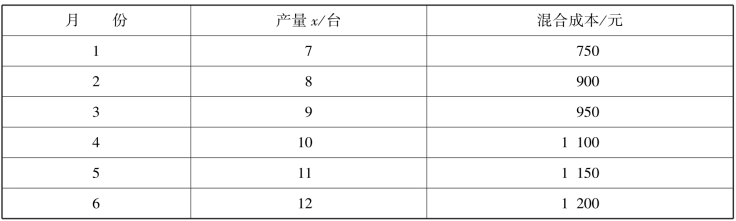
解：将6 期的成本点坐标分别标在坐标纸上，形成散布图，如图2-10所示。该直线的截距a＝200；在直线上任取一点P，测出它的坐标为（10，1 050），则有

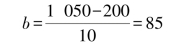
答：该项混合成本的性态模型为y＝200＋85x。

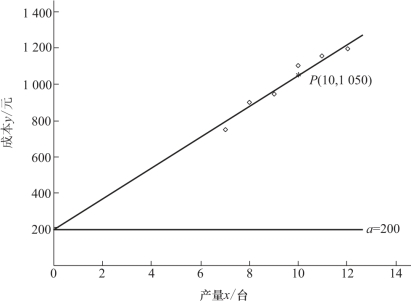
图2-10　散布图

可见，该方法导出的公式仍为y＝a＋bx。从理论上讲，图上的每一点应当与斜线重合，但许多点却分布在斜线两侧，因此，它只是说明一种变动趋势，并不能保证每一点都很精确地在这条直线上。该方法的优点是简易、形象、直观，比只要两头不要中间的高低点法更为精确。但由于按目测画线，客观上存在一定误差。

采用散布图法应注意两点：一是将成本数据精确地标在坐标纸中；二是目测成本变动趋势，根据该趋势描绘一直线，力求该直线最大限度地表达变动趋势，使误差达到最小。

3）一元直线回归法

一元直线回归法，是根据过去若干期业务量和成本的数据，运用最小二乘法原理建立反映业务量和成本之间关系的回归直线方程，并计算成本中的固定成本（或混合成本中的固定部分）a 和单位变动成本（或混合成本中变动部分的单位额）b 的一种成本性态分析方法，又称最小二乘法或最小平方法。

一元直线回归法的计算结果比前两种方法更准确、科学，但计算量大，公式复杂。

一元直线回归法的具体步骤是：

①根据历史资料列表，求n、∑x、∑y、∑xy、∑x2和∑y2的值。

②按下式计算相关系数r，并据此判断y 与x 之间是否存在必要的内在联系：

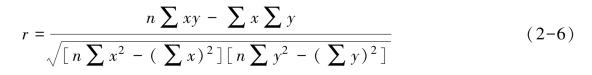
相关系数r 的取值范围一般在0 与±1 之间，它可说明x 与y 之间的密切程度：当r＝-1时，说明x 与y 之间完全负相关；当r＝0 时，说明x 与y 之间不存在任何联系，为零相关，即y≠a＋bx；当r＝＋1 时，说明x 与y 之间完全正相关，即y＝a＋bx；当r→＋1，说明x 与y基本正相关，可近似地写成y＝a＋bx 的形式。一元直线回归法要求业务量x 与成本y 之间基本上保持线性关系，否则研究无意义。

③按照下列公式求a、b 值：

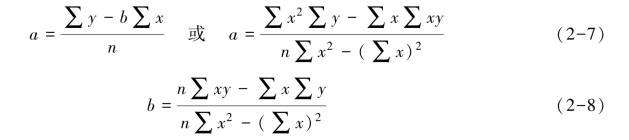
④将a、b 值代入下式，写出一般成本性态模型：

y＝a＋bx

【例2-7】仍以【例2-5】中的表2-3 资料为例，要求用一元直线回归法进行成本性态分析。

解：根据表2-3 的资料加工整理，计算n，∑x，∑y，∑xy，∑x2，∑y2 的数值，如表2-5所示。

表2-5　n，∑x，∑y，∑xy，∑x2，∑y2 的计算

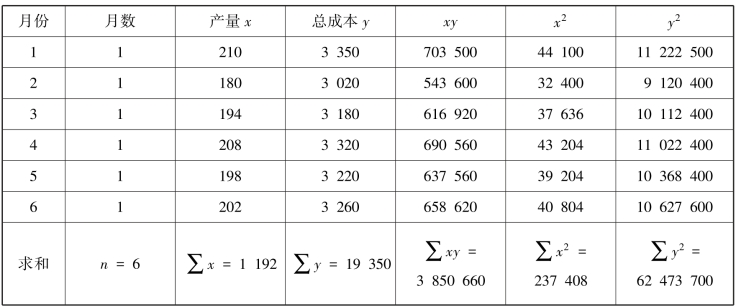
将表中的数据代入相关系数的计算公式中。

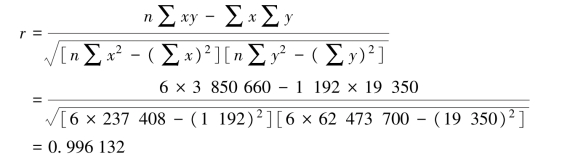
由于r 的值接近于1，即说明x 与y 之间具有密切的相关关系，基本上属于线性关系，所以可用y＝a＋bx 的直线来描述其变动的趋势。

应用一元直线回归法确定b 和a 的值：

将a、b 值代入y＝a＋bx，可写出一般成本性态模型：y＝1 076.61＋10.81x

答：该成本性态模型为y＝1 076.61＋10.81x，其中固定成本部分为1 076.61，变动成本部分为10.81x。

一元直线回归法利用了微分极值原理，因此计算结果比前两种方法更为准确，但计算工作量较大，比较麻烦。如果能使用电子计算机计算，这种方法将会得到广泛应用。

4）财务分析法

账务分析法是指会计人员根据其经验，对有关记录各项成本费用支出的账户进行分析、判断，将各项成本划归为固定成本与变动成本的方法。这种方法工作量较大，必须对每一项支出进行判断。