1）定义

模糊综合评价方法是模糊数学中应用的比较广泛的一种方法。在对某一事务进行评价时常会遇到这样一类问题，由于评价事务是由多方面的因素所决定的，因而要对每一因素进行评价；在每一因素作出一个单独评语的基础上，如何考虑所有因素而作出一个综合评语，这就是一个综合评价问题[98-99]。

2）模糊评价的基本思想

许多事情的边界并不十分明显，评价时很难将其归于某个类别，于是我们先对单个因素进行评价，然后对所有因素进行综合模糊评价，防止遗漏任何统计信息和信息的中途损失，这有助于解决用“是”或“否”这样的确定性评价带来的对客观真实的偏离问题。

3）模糊评价基本模型

设评判对象为P：其因素集评判等级集。对U中每一因素根据评判集中的等级指标进行模糊评判，得到评判矩阵：

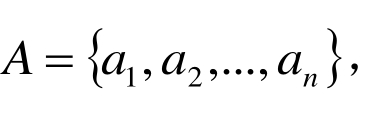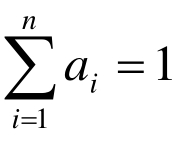其中，rij表示ui关于vj的隶属程度。（U，V，R）则构成了一个模糊综合评判模型。确定各因素重要性指标（也称权数）后，记为满足，合成得

经归一化后，得于是可确定对象P的评判等级。

置信度模糊评价模型

（1）置信度的确定

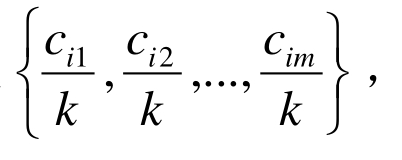在（U，V，R）模型中，R中的元素rij是由评判者“打分”确定的。例如 k 个评判者，要求每个评判者uj对照作一次判断，统计得分和归一化后产生且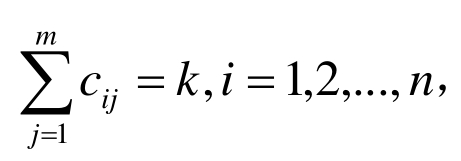组成 R0。其中既代表 uj关于vj的“隶属程度”，也反映了评判uj为 vj的集中程度。数值为1，说明 uj为 vj是可信的，数值为零为忽略。因此，反映这种集中程度的量称为“置信度”。对于权系数的确定也存在一个信度问题。

在用层次分析法确定了各个专家对指标评估所得的权重后，作关于权系数的等级划分，由此决定其结果的信度。当取N个等级时，其量化后对应于[0，l]区间上N次平分。例如，N取5，则依次得到[0，0.2]，[0.2，0.4]，[0.2，0.6]，[0.6，0.8]，[0.8，l]。对某j个指标，取遍k个专家对该指标评估所得的权重，得。作和式(www.daowen.com)

其中dij表示数组中属于的个数，。

取

取遍得，归一化后得到权向量。如果则 ai的信度为。由此得信度向量为。

（2）置信度的综合

设c1，c2是二个置信度，对于逻辑AND，其信度合成为

对于逻辑OR，信度成为

其中｛ε∈[1，0]为参数，可适当配置。（5）、（6）二式的含义是：在逻辑 AND 下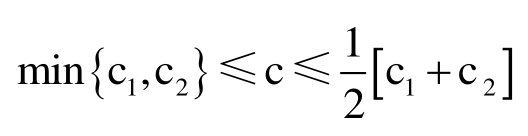，；在逻辑OR下，。若c1<1或c2<1，则（5）、（6）二式中的平均值补偿部分不宜太强。ε可如下配置：

对于（2）式信度合成为：

其中：

εi和εj的选择可参照（7）式。

结合（2）式，得到信度的评判结果：