对于上述博弈模型，有两种情形的解可以讨论。

一是车企最优:即对于所有C∈[0，1]，S*a(C)是下列最优化问题的解:

在这里，E[Sb(P)｜Sb(P)≥Sa]是给定车企对政府投资数额的预测低于实际政府投资数额的条件下，车企对政府投资数额的预测情况。

二是政府最优:即对所有的P∈[0，1]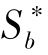，(P)是下列最优化问题的解:

Prob{Sb≥Sa(C)}

这里，E[Sa(C)｜Sb≥Sa(C)]是给定车企对政府投资数额的预测低于实际政府投资数额的条件下，政府对车企所投入的成本的预测情况。

不难看出，这个博弈模型中会存在多个贝叶斯均衡。首先我们考虑如下的线性战略均衡情况:

Sa(C)＝αa+βaC(www.daowen.com)

Sb(P)＝αb+β(P)

因为P在[0，1]上均匀地分布，因此，Sb在[αb，αb+βb]上均匀地分布。因此，通过推导和演算，可以得出最优化的一阶条件:

这样的结果可以证明，如果政府对新能源汽车的投入选择的是线性战略，那么，车企的最优反应也是线性的。

同上所述，因为C在[0，1]上均匀地分布，Sa在[αa，αa+βa]上均匀地分布，通过推导和演算，可以推出最优化的一阶条件:

解上述所得出的两个一阶条件可得均衡线性战略为:

在均衡的状况下，当且仅当αb+βbP≥αa+βaC，或者说P≥C+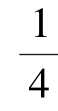时，政府和车企双方才会对新能源汽车的发展产生浓厚的兴趣从而促使新能源汽车产业链的发展。通过这样的结论我们可以发现，在线性战略的情况下，政府投资和车企投入成本的关系是明显可以预见的。又由于政府对新能源汽车产业链发展的投资会起到一定的主导作用，所以政府对新能源汽车产业链的投入必须大于车企所投入成本的5/4，且政府可以根据自己所投入的额度来引导车企投入成本的大小。根据这个模型所得出的结论，值得政府对新能源汽车的投入进行深度思考。

上述关于此博弈模型的讨论都是针对有关政府和车企的线性战略均衡情况来展开的。当然，这个博弈模型还有许多其他的贝叶斯均衡。但是已经有著名学者证明过在均匀分布的情况下，线性战略均衡比其他任何贝叶斯均衡所产生的净剩余都高。这就意味着线性战略均衡对于政府和车企双方来说，如果没有特别的信息因素干扰，或者双方任何一方都没有获得能够准确预测对方投入的精准信息的情况下，那么为了使得新能源汽车产业链能够产生的净效益最大，双方都会选择线性的战略。从而，在此博弈中占主导作用的政府对新能源汽车产业链的投入情况便可以被政府作为政策变量引入，从而选择合理的投入额度来引导和鼓励新能源汽车产业链的发展。