“一寸光阴一寸金”本是一句劝人惜时的谚语，但在理财活动中，这就是现实，今天的一元钱和一年后的一元钱其经济价值不相等，现在的一元钱比一年后的一元钱经济价值大些，即使不存在通货膨胀也是这样。

西德尼·霍默（Sidney Homer）在《利率的历史》中举过一个例子：假如将1 000美元按8%的年利息存入银行，400年后，这笔钱从银行取出将变成2.34×1016美元，这个简单的例子直观地显示了货币时间价值的威力。

【例】某企业现用25万元购买国库券，年利率4%，一年后可得本利和26万元（25＋25×4%）。

将25万元作为资本，经过一年时间的投资增加了1万元，这就是资金的时间价值。

【例】某人拟购买一套商品房，若采用现付的方式，价格为120万元，如延期3年后付款，价格为136万元，且3年银行利率5%，假定为单利，不考虑其他因素，此人该采用哪种付款方式呢？

假设此人现在已有120万元现金，他将钱存入银行，3年后单利计算得本利和为138（120＋120×5%×3）万元，同136万元比较，他还可以得到2万元的利益，说明随着时间的推移，周转的资金发生了增值。因此，他应选择延期3年后付款。

通过以上分析可以得出如下结论：

1．相同量的货币在不同时点上反映的价值是不同的。

2．等量的货币随时间推移而增值，越靠前的货币越值钱。

货币的时间价值就是资金在周转使用中由于时间因素而形成的差额价值。

在具体应用之前，需要介绍一些基本概念和公式。

1．终值和现值

终值就是未来值，是将一定量货币在将来某个时候的价值，俗称本利和。现值又称本金，是将来某一时刻一定量现金折合到现在的价值。

2．单利和复利

单利是指不论时间长短，其所生利息不加入本金计算利息，即利不能生利。

复利俗称“利滚利”，它是指不仅本金计算利息，而且本金所生的利息在下期也转入本金，再计算利息，即，本能生利，利亦能生利，实际上，时间价值一般按复利计算。

3．货币时间价值具体计算

为方便起见，本章在介绍资金时间价值的计算方法时假定有关字母含义如下：

F——终值（本利和）

P——现值（本金）

A——年金

i——利率（折现率）

n——计息期数

i和n应互相配合，如i为年利率则n为年数，i为月利率，n则为月数。

单利终值计算公式：

F＝P×（1＋i×n）

单利现值计算公式：

复利终值计算公式：

F＝P×（1＋i）n＝P（F/P，i，n）

复利现值计算公式：

式中，（1＋i）n称为“一元的复利终值系数”记为P（F/P，i，n），可查“一元的复利终值系数表”求得，见附表一。

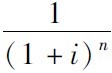称为“一元的复利现值系数”记为F（P/F，i，n），可查“一元复利现值系数表”求得，见附表二。

【例】某公司将80 000现金存入银行，存款利率为5%，存款期为3年，按复利计算。

到期本利和为：

F＝P×（1＋i）n＝80 000×（1＋5%）3＝80 000×（F/P，5%，3）

＝92 680（元）

【例】某投资项目预计5年后可得收益500万元，按年利率10%计算，按复利计算，问这笔收益现在价值是多少？

4．年金

年金是指一定时间内等额、定期的系列收付款项。需要指出的是，系列等额收付的间隔期只要满足相等条件即可，即，间隔期完全可以不是一年。年金有多种形式，根据第一次收到或付出资金的时间不同和延续时间长短，可分为普通年金、即付年金、永续年金、递延年金。

在企业经营活动中，按直线法计提的折旧、租金、保险费、利息等通常都采用年金的形式。

（1）普通年金。普通年金也称后付年金，即在每年期末收到或付出的年金，在现实中，这种年金是最常见的。

普通年金终值的计算公式：

式中，（F/A，i，n）称为“年金终值系数”，可通过直接查阅“1元年金终值系数表”求得有关数值。

普通年金现值的计算公式：(www.daowen.com)

式中，称为“年金现值系数”，同样可通过直接查阅“1元年金现值系数表”求得有关数值。

（2）即付年金。即付年金又称先付年金，即在每期期初收到或付出年金。它与普通年金的区别仅在于收付时间不同。

即付年金终值的计算公式：

即付年金现值的计算公式：

（3）递延年金。递延年金是指第一次收到或付出发生在第二期或第二期以后的年金。即第一次收付与第一期无关，而是隔若干期后才发生的系列等额收付款项。简言之，凡不是在第一期开始的年金都是递延年金，它是普通年金的特殊形式。

递延年金终值计算与普通年金计算一样，只是要注意期数。计算公式如下：

F＝A×（F/A，i，n）

需要指出的是，式中，“n”表示A的个数，与递延期无关。

递延年金现值计算公式：

公式一：

P＝A×[（P/A，i，m＋n）－（P/A，i，m）]

公式二：

P＝A×[（P/A，i，n）×（P/F，i，m）]

公式三：

P＝A×[（F/A，i，n）×（P/F，i，m＋n）]

式中，m为递延期，n为连续实际发生的期数。

方法一，是假设递延期中也进行收付，先求出（m＋n）期的年金现值，然后扣除实际并未收付的递延期（m）的年金现值，即可得到最终结果。

方法二，是把递延年金视为普通年金，求出递延年金的现值，然后再将此现值调整到第一期期初。

方法三，是先求出递延年金的终值，再将其折算为现值。

需要说明的是，这三种方法第一次发生均在m＋1期期末。

（4）永续年金。永续年金，即无限期等额收入或付出的年金，可视为期限趋于无穷大的普通年金。存本取息可看做永续年金的计算，永续年金没有终止时间，因此也没有终值，只有现值。

永续年金现值计算公式：

当n→∞时，（1＋i）－n极限为0，故上式可写作：

5．货币时间价值在实际中的具体应用举例

（1）工程结算问题。

【例】某企业进行某项在建资产，在三年建设期内每年年末向银行借款10万元，借款年利率为10%，问该项目竣工后应付本利和为多少？

F＝A×（F/A，i，n）＝10×（F/A，10%，3）＝10×3.31＝33.1（万元）

（2）偿债基金问题。

【例】拟在10年后还清2 000 000元债务，从现在起每年末等额存入银行一笔款项，假设银行利率为4%，每年需要存入多少元？

（3）财产保险问题。

【例】某公司准备实行财产保险，从第4年开始缴纳保险费，每年年末缴纳50万元，保险到第10年末，若年利率为10%，试求公司现在存入银行多少钱以备到期支付保险费？

P＝A×[（P/A，i，m＋n）－（P/A，i，m）]

＝50×[（P/A，10%，10）－（P/A，10%，3）]

＝50×（6.145－2.487）

＝182.9（万元）

（4）设备使用期限。

【例】某企业拟购买一台新设备，更换旧设备，新设备较旧设备高出2 000元，但每年可节约成本500元，若利率为10%，问新设备应至少使用多少年对企业而言才有利？

已知P＝2 000，A＝500，i＝10，则：

（P/A，10%，n）＝P/A＝2 000/500＝4

查i＝10%的普通年金现值系数表，在i＝10%一列上无法找到相应的利率，于是在该列上寻找大于和小于的临界系数值，分别为，β1＝4.3553α＝4，β2＝3.7908α＝4。同时，得到临界利率为n1＝6，n2＝5。则

即新设备最少要用5.4年对企业而言才有利。

马克思曾说过：作为资本的货币的流通本身就有目的的，因为只有在这个不断更新的过程中才有价值增值。因此，要想使自有的资金保值和增值，就必须将其融入资金流通过程，这也正是所谓的“钱能生钱”。

对企业财务管理人员而言，重要的是要接受货币时间价值观念，重视时间价值在资金流通中的影响，从而能够选择最合理的资金运用方式。