物流企业以契约模式为基础，同时为其他物流企业提供服务。对于物流企业的提供方和需求方，其之间的交易存在时间上的延迟。所以，深入了解彼此之间的信用水平、信用度显得尤为重要。物流企业的服务商与客户之间需要以信任为基础，建立融洽和谐的合作关系，才能为其提供多样化的服务，为顾客创造更多的价值，最终达到“双赢”的目的。本书在充分了解物流企业特点的基础上，深入研究了影响物流企业信用评价的因素，并构建了一套物流企业信用评价体系，希望可以为规范物流行业信用水平提供依据，同时可以加快物流行业的高效快速发展。信用评价也称为信用评估、信用评级、资信评估、资信评级等，它是对各类企业所负各种债务能否如约还本付息的能力和可信任程度的评估，是一个具有因素多、标准不一等特点的问题。常用的信用评价方法有因子分析法、数据包络分析法、层次分析法以及以上多种方法相结合的方法。

从信用评价诞生之后的一个多世纪中，全球各个国家都不断地对信用方法及评价模型进行分析研究。在信用评价中，最重要的是对被评价行业的评价指标因素进行确定，选择相应的信用评价模型，将多个评价指标综合起来，进行权重的赋值，并最终形成一定的信用评价体系。

1.信用评价的相关方法

信用评价方法，一般情况下经常使用的有多元判别分析模型、回归分析法、人工神经网络法和层次分析法等。

1）多元判别分析模型（MDA）

多元判别分析模型是对企业多个财务比率进行汇总，求出一个总判别分值来预测企业财务危机的模型。最早在20世纪，Edward.Altman首次运用判别分析法对企业的信用评价情况进行分析，通过收集大量数据，筛选了22个财务指标作为研究变量，并选择其中最具有代表性的5个指标作为研究基础，5个指标分别是X1=营运资本/总资产；X2=留存收益/总资产；X3=息税前收益/总资产；X4=权益账面价值/账面债务总额；X5=销售收入/资产总额，并建立了Z模型，见公式（5.2）：

Z模型的运用需要对大量的财务数据进行统计整理和分析，但有些数据很难获得，因此AlexanderBathory在Z模型的基础上，建立了Bathory模型，该模型使计算更加的简便，使数据更易获得，同时不仅可以预测企业破产的可能性，还可以将企业的实力一起预测出来，见公式（5.3）：

但是，在实际操作过程中，无论是Z模型还是Bathory模型，都存在着一定的缺陷：一方面，在信用评价过程中，对于评价指标的确定，上述模型法更多的是以企业财务报表为基础来获得财务数据的相关信息，忽略了市场经济活动中的其他指标因素，从而使评价结果的准确率降低；另一方面，在多元判别法的运用过程中，需要调查的数据服从正态分布，但现实市场经济活动中，数据信息是很难呈正态分布的，所以，最终做出的信用评价结果难免存在不准确性。

2）回归分析法

为了消除多元判别法对数据服从正态分布的依赖，Martin在1977年建立了Logistic回归模型，西方一些专家借用Logistic函数建立了LogisticRegression信用评分模型。回归分析模型主要解决的是0-1回归问题，该模型假设信用危机发生的概率是p，同时假设ln［p/（1-p）］可以通过财务比率来线性表示，见公式（5.4）、公式（5.5）：

3）人工神经网络法

人工神经网络法是以认知科学和神经心理学为基础的，同时将数学方法引入其中来进行运算，因此它具备较高的计算能力和容错能力。神经网络的应用最初是由Tam（1991）、Kiang（1992）、Dutta、Shekhar（1992）建议用于银行破产的预测的。神经网络的结构通常可以分成三部分：输入层、中间隐含层以及输出层。

神经网络方法最大的优势是运算，它选择模型时比较简便，另外避免了线性模型带来的限制，所以它是一种非线性模型。它可以使评估模型的建立过程更加方便快捷。但是，不可否认的是，人工神经网络法也存在着一定的不足：一方面，它的工作随机性比较强，这样就会使评价结果存在不稳定性；另一方面，如果想要构建一个比较优秀的神经网络结构，我们就需要消耗大量的人力、物力、财力来进行调试，这样造成了成本的增加。所以，这个方法在社会中的普及受到了一定的制约。

4）层次分析法（AHP）

层次分析法，最初是在20世纪70年代由美国运筹学家T.L.Saaty提出的。该方法主要是通过对比较复杂的问题进行详细的研究，主要研究其因素之间的关系，然后使用少数代表性比较强的因素来进行最终决策。

2.层次分析法简介

层次分析法（AHP）是由美国数学家萨蒂提出并逐步完善的一种简易实用的决策方法。它是一种分析多目标、多准则量化、将人脑分析方案的过程数学化、定性与定量相结合的系统分析方法。这种分析方法的特点是在对复杂决策问题的本质、影响因素、内在关系进行分析研究的基础上，利用比较少的定量信息使决策的思维过程数学化，从而最终为多目标、多准则以及无结构特性的复杂决策问题提供简单方便的决策支持方法。层次分析法把研究对象作为一个系统，按照分解、比较判断、综合的思维方式进行决策，成为继机理分析、统计分析之后发展起来的系统分析的重要工具。对于“方案层+因素层+目标层”构成的递阶层次结构决策分析问题，AHP给出一整套的处理方法。另外，AHP把定性方法和定量方法有机地结合起来，使复杂的系统分解，能将人们的思维过程数学化和系统化，便于人们接受。

运用层次分析法进行评价或决策时，大体分为四步：①明确问题，建立层次分析法的层次结构评价模型；②构造判断矩阵；③层次单排序及其一致性检验；④层次总排序及其一致性检验。

1）建立层次结构模型

运用层次分析法解决问题时，首先要将问题条理化、层次化，构建一个有层次的结构模型。这种层次结构中包括最高处、中间层和最底层，层次结构模型示意图如图5.14所示。

最高处：该层是目标层，表示解决问题的目的，即层次分析要达到的总目标。一般情况下只有一个目标，若有多个分目标的时候，我们可以在最高目标层下面继续再建立一个分目标层。

中间层：该层包括准则层以及指标层。它表示采取了某一方案来实现预定的总目标所涉及的各项准则和指标。

最底层：该层是方案层，它代表要选用的解决问题的各种措施、策略和方案等。

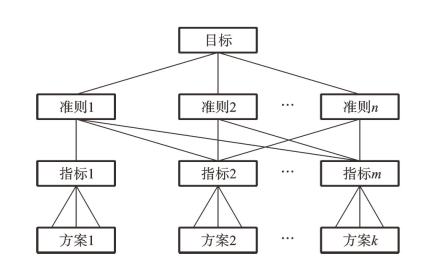
图5.14　层次结构模型示意图

2）构造判断矩阵

层次分析法的一个重要特点就是用两两重要性程度之比的形式表示出两个方案的相应重要性程度等级。判断矩阵如表5.8所示。(www.daowen.com)

表5.8　判断矩阵

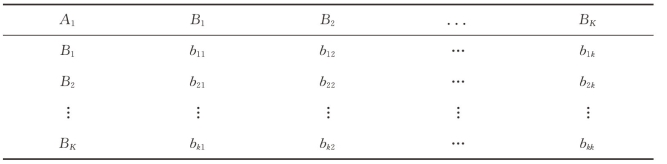
在判断矩阵中，A，为上一层元素，Bi为本层次元素，bij表示相对于上一层的元素Ai、Bi和Bj相对比的重要性程度。根据对人的心理特征和思维规律的研究，AHP法一般采用的是9种标度来确定bij的值，9种标度的含义如表5.9所示。

表5.9　9种标度的含义

说明：

（1）判断矩阵的个数等于上一层元素的个数。

（2）判断矩阵的元素bij取值为9种标度的值或其倒数。

（3）判断矩阵中对角线元素的值是1，其他元素满足：bij=。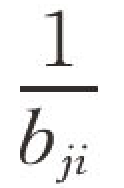

3）层次单排序及其一致性检验

层次单排序是指每一个判断矩阵其各个因素针对其准则的相对权重，本质上是计算权向量。计算权向量的方法有特征根法、和法、根法、幂法等，这里主要介绍和法。和法的基本原理是，对于一致性判断矩阵，每一列归一化后就是相应的权重。对于非一致性判断矩阵，每一列归一化后近似其相应的权重，最终再对这n个列向量求算术平均值，来作为最后的权重。具体的公式见公式（5.6）：

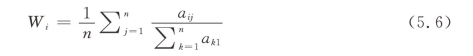
另外，在层次排序中，我们必须要对判断矩阵进行一致性检验。在特殊情况下，判断矩阵可以具有传递性和一致性。但在一般情况下，并不要求判断矩阵严格满足这一特殊性质。从人类认识规律看，一个正确的判断矩阵的重要性排序是有一定逻辑规律的，例如如果A比B重要，B又比C重要，则从逻辑上讲，A应该比C明显重要，若两两比较时出现C比A重要的结果，则该判断矩阵违反了一致性准则，则认为在逻辑上是不合理的。因此在实际进行排序时，我们要求判断矩阵必须满足大体上的一致性，也就是说，需要进行一致性检验。只有通过了检验，才能证明判断矩阵在逻辑上是合理的，最后才能继续对计算结果进行分析。

进行一致性检验的操作步骤如下。

第一步，计算一致性指标CI（Consistency Index），见公式（5.7）：

第二步，查表，确定相应的平均随机一致性指标RI（Random Index）。

根据判断矩阵的不同阶数，查表5.10，可以得到RI（平均随机一致性指标）。

表5.10　与1～9阶矩阵相对应的RI值

第三步，计算一致性比例CR（Consistency Ratio），并进行一致性检验的判断，见公式（5.8）：

当CR＜0.1时，我们认为判断矩阵的一致性是可以接受的；当CR＞0.1时，我们认为判断矩阵是不符合一致性检验要求的，需要对该判断矩阵进行重新的修改以最终使得CR＜0.1。

4）层次总排序及其一致性检验

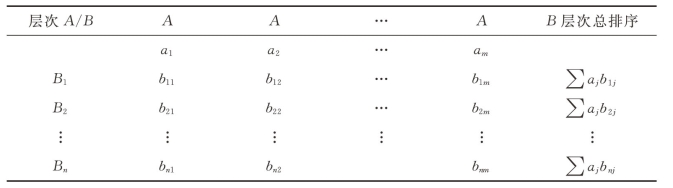
这一步骤是从高到低，逐层进行的。利用同一层次的层次单排序结果，可以计算针对上一层次而言，本层次所有影响元素重要性的权值。假设上一层次的所有元素A1，A2，…，Am的层次总排序已经完成，得到的权值是a1，a2，…，am，与Aj对应的本层次元素B1，B2…，Bn，其单排序的最终结果是b1j，b2j，…，bni，层次总排序表如表5.11所示。

表5.11　层次总排序表

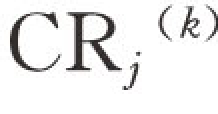同层次单排序相同，层次总排序也需要进行一致性检验。假设已经算出了针对第k-1层的第j个元素为准则的、和，j=1，2，…，m，那么第k层的综合检验指标，见公式（5.9）、公式（5.10）、公式（5.11）：

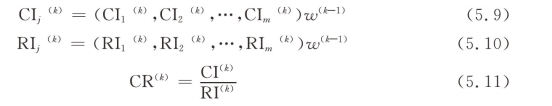
当CR（k）＜0.1时，认为判断矩阵的整体一致性是可以接受的。