未来，关于概率不确定语言术语集多准则群决策方法的研究应着重以PULTS的信息融合方法和测度理论框架为基础，研究PULPR的一致性-共识达成过程以及一系列基于PULTS的群决策方法、大规模群决策方法及其应用。

1.PULTS的信息融合方法、测度理论框架研究

（1）PULTS的运算法则及比较规则。PULTS由多个概率不确定语言元素（PULTE）组成，不确定语言变量与其对应的概率信息的含义不同，在定义运算时难以论证不确定语言变量上、下限标度与概率直接相乘的合理性，而且运算结果可能会超出语言术语集的边界，同时需要考虑定义在非平衡语言术语集上PULTS的运算问题。因此，为保证PULTS运算的合理高效，避免运算结果违背直觉或超出语言术语集的边界，同时考虑到处理非平衡语言术语集的运算需求，几种有针对性的运算法则及比较法则被定义出来：①基于不同语言术语集的语义结构特征，三种不同类型的等价语言标度函数对语言术语进行转换；针对概率调整后PULTE成对比较的PULTS定义运算法则、期望值及方差；②基于OWHFS与PULTS的可逆转换，在运算法则定义中以规范化概率权重体现概率信息并提供比较规则；③根据PULTS的分布特征提出运算规则并提出PULTS比较的可能度公式；④基于Archimedean T模和T-余模、语言标度函数定义运算法则及其特殊形式。

（2）基于决策要素关联性或独立的PULTS信息集成算子。受HFLTS、PLTS信息集结算子研究的启发，结合PULTS自身的结构特征，基于决策要素独立性假设，研究概率不确定语言加权平均（PULWA）算子、概率不确定语言加权几何平均（PULWGA）算子、概率不确定语言有序加权平均（PULOWA）算子或概率不确定语言有序加权几何平均（PULOWGA）算子等。根据被集结PULTS的关联性，提出一系列考虑PULTS交互作用的信息集成算子：①提出概率不确定语言几何Bonferroni Mean（PULGBM）算子、加权概率不确定语言几何Bonferroni Mean（WPULGBM）算子并推导各算子的具体表达式；②Power平均算子和几何算子能使被集结信息之间相互支持或补偿强化，结合PULTS的支持度，提出概率不确定语言Power平均（PULPA）算子、概率不确定语言Power几何平均（PULPGA）算子；考虑被集结信息的权重，提出加权概率不确定语言Power平均（WPULPA）算子、加权概率不确定语言Power几何平均（WPULPGA）算子；③提出概率不确定语言Archimedean Muirhead Mean（PULAMM）算子及其加权算子、概率不确定语言Archimedean dual Muirhead Mean（PULADMM）算子及其加权算子，包含这几类算子的退化形式。

（3）PULTS的距离测度、相似性测度及关联测度。从代数距离及几何距离的角度定义PULTS的距离测度与相似性测度：在PULTS距离测度公理化定义的基础上，定义PULTS的Hamming距离、Euclidean距离及广义Hausdorff距离及相似度，同时提出这几种距离测度的混合形式、广义形式与退化形式；由PULTS与最大化PULTS的距离定义距离测度及广义的Hausdorff距离。基于加权距离算子，研究离散、连续两种情形下PULTS序列的加权距离、有序加权距离。提出PULTS的模糊熵、犹豫熵、交叉熵及总熵测度的概念、具体表达式。根据反映不同语义分布特征的语言标度函数提出PULTS的关联测度；基于PULTS的熵值及交叉熵提出PULTS的关联测度。

2.基于概率不确定语言的一致性-共识达成过程及决策方法研究

（1）基于PULPR一致性检验、提升及共识达成的群决策方法。

Step3：确定方案排序的两种思路：①针对达成共识的所有NPULPRs，利用PULWA算子或PULWGA算子得到群体PULPR，根据PULOWA算子或PULOWGA算子获取各方案的综合偏好值，由比较规则得到各方案排序结果；②构造综合PULPR的余弦相似度最大化的线性规划模型确定优先权重向量，从而得到方案优劣次序。

（2）基于案例推理及PULPR积性一致性达成的决策方法。

Step3：根据各准则权重得到各方案的综合获得优势得分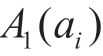并降序排列，同时得到基于“群效用值”的方案次序集；定义加权最大化损失优势得分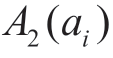并升序排列，由各方案最大化“个体遗憾值”得到次序集；为保证集结所得最终排序结果的稳健性，考虑各方案的两种优势得分及其次序，将每个方案的次序转换为对应规范化优势得分的权重，得到融合结果，从而确定最优方案。

3.基于PULTS的多准则群决策方法研究

（1）基于PUL-LINMAP的多准则群决策方法。

Step2：根据成对比较方案的加权偏差平方构造每个决策者下两两方案间的一致性系数和不一致性系数，从而得到所有决策者关于方案之间成对比较的综合一致性系数和综合不一致性系数。基于“综合不一致性系数应当趋近于0，且综合不一致性系数应当不比综合一致性系数大”的原则，构建线性规划模型并利用软件包求解得到各准则权重，从而获取各决策者下每个方案与PULPIS的加权偏差平方，得到单个决策者关于所有方案的排序结果。

Step3：利用Borda函数求得群体关于所有方案的优劣次序。通过算例分析说明PUL-LINMAP方法的有效性及可行性，同时与基于PULWA算子的决策方法或PLTS决策环境中PL-PROMETHEE方法进行对比分析，论证PULLINMAP方法的特点及适用领域。

（2）基于扩展VIKOR法、TODIM法的概率不确定语言多准则群决策方法。

Step1：将各决策者提供的不确定语言评价融合得到以PULTS表示的群决策矩阵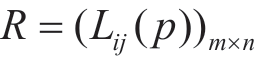，并规范化处理得到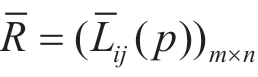。确定各准则权重有两种思路：①计算各准则值的得分函数值，并将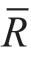转化为以得分函数值表示的转换矩阵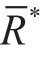，基于熵权法确定各准则权重；②根据扩展Hausdorff距离采用离差最大化法确定各准则权重。

Step3：经算例分析验证决策方法的有效性及可行性，通过仿真模拟分析TODIM法中参数θ的变化对排序结果的影响，并与已有群决策方法进行对比，探讨排序结果的异同及造成差异的原因。

（3）基于概率不确定语言ORESTE法的多准则群决策方法。

4.基于PULTS的大规模群决策方法研究

（1）基于PULTS及决策分组权重未知的大规模群决策方法。(www.daowen.com)

（2）多领域利益相关者参与的不完全多粒度PULTS大规模群决策方法。

Step1：多领域利益相关者构成的大规模决策群组通过问卷调查或访谈的方式，基于给定的不同粒度语言术语集对每个备选方案给出各准则的不完全多粒度的不确定语言评价值，经统计得到各决策分组针对每个方案以不同粒度PULTS表达的准则信息。

Step2：将不同粒度表达的PULTS转化为同一粒度，根据决策者对待风险的态度将PULTS矩阵进行规范化处理；随后根据实际决策需求，将以语言术语表达的等概率或非等概率决策者权重与PULWA算子融合得到群决策矩阵；

Step3：针对准则权重完全未知或不完全已知的情形，采用离差最大化法确定各准则权重，基于扩展TOPSIS法对各方案排序；分析决策者的不同风险态度对决策结果的影响，同时与已有大规模群决策方法进行对比。

（3）基于PULTS大规模群决策方法的城市群生态环境治理效率评价。

Step1：依托大数据技术从生态环境部、国家统计局等国家部委公开的数据信息中采集并筛选出近三年有关城市群区域生态环境治理状况的定量化数据。主要针对京津冀城市群、长三角城市群、粤港澳大湾区等9个已获批的国家级城市群展开评估，构建城市群生态环境治理效率评价指标体系，指标体系中的定性指标拟邀请生态环境治理专业领域的专家采用不确定语言评价给出。

Step2：将参与定性指标评价的专家按领域分组，将各分组提供的不确定语言信息融合得到以PULTS表达的评估信息；同时依据指标体系将大数据驱动下的定量化数据与PULTS信息合并，并分别进行规范化预处理。

Step3：针对各城市群的混合评估信息，计算各城市群数据序列的相关系数，经聚类分析得到关于环境治理效率的城市群分类，参照采集的定量化数据探索各聚类的特征。

Step4：在聚类分析的基础上，拟采用基于PULTS的混合型大规模群决策方法获取各城市群生态环境治理效率状况的排序结果，并结合聚类分析结果提出新时期提升各城市群生态环境治理效率的应对策略。

5.基于PULTS的多准则群决策方法的应用研究展望

为应对现实决策问题的复杂不确定性以及参与决策过程的多领域利益相关者思维的犹豫模糊性，满足实际决策需求，近年来，基于PLTS的多准则群决策方法已经应用到“一带一路”沿线国家投资风险评价、针对病患的个性化医院推荐选择和医疗体系评价、使用户满意度最大化的熊猫共享汽车创新设计方案选择问题、基于旅游者在线评论的Trip Advisor网站酒店选择决策、石化企业突发火灾事故的应急决策、雄安新区等三个新区的发展前景评估、人工湿地的可持续性发展评价问题、脑转移性非小细胞肺癌的治疗方案优选等方面，已有应用研究充分发挥了概率语言术语集对偏好信息灵活性、可解释性和可信度较高的表达优势，应用研究领域广泛，突显出良好的应用效果及研究价值。

相对于概率语言术语集，采用PULTS既能更为高效、精准地反映定性决策信息的模糊不确定性，又能获取不确定语言评价下的概率信息，表征出特定对象所有可能评估值的不同重要程度，保留了更为详细的决策信息。考虑到PULTS对偏好信息的表达优势，以下给出基于PULTS多准则群决策方法的应用研究展望。

（1）风险投资项目评估及项目选择问题。现有风险投资的多准则群决策方法往往忽略风险投资者相互作用下信息表达的不确定性，因此有必要采用PULTS对各准则间的权重分布以及风险资本之间的权重分布进行清晰地描述，既考虑到风险投资者之间的交互作用关系，也考虑到风险投资者与风险项目承包人之间的交互作用，能够提供更为完整的投资项目评估信息。在该研究领域，PULTS展现出了较为明显的优势。

（2）水安全评价及水污染防治问题。将基于PULTS的多准则群决策方法应用到该领域，能够使用多种不确定语言及其概率信息表达水安全评价指标，PULTS通过反映各决策者对水安全状况的主观判断和精细化偏好程度体现各决策者对实际水安全问题的有限理性行为特征，这恰恰能够体现出PULTS决策方法在该应用领域的研究优势；同时为水污染防治问题提供针对不同地域的精准化治理策略。

（3）基于产品在线评论的消费者购买决策问题。虽然基于PLTS的多准则群决策方法已经应用到该领域并产生了一些研究成果，但拓展到PULTS后，对产品在线评论信息的挖掘更为深入细致，兼顾消费者的不完全理性和评价准则间存在的交互作用，进一步优化了产品购买决策评估的准则指标体系。在网络意见环境下，潜在消费者可以通过产品性能评价来评估产品的品质优劣，最终做出理性的购买决策。

（4）城市群生态环境治理效率评价问题。在京津冀城市群、长三角城市群、粤港澳大湾区等城市群推动国家重大区域战略融合发展的背景下，为响应新时代生态文明建设的总体要求，拟对已批复的9个国家级城市群的生态环境治理效率进行评价。可采用如下研究思路：依托大数据技术构建城市群生态环境治理效率评价指标体系，对各城市群生态环境治理效率状况进行聚类分析，并利用基于PULTS的大规模群决策方法获取各城市群排序结果，最后提出新时期提升各城市群生态环境治理效率的应对策略。

（5）基于PULTS或PULPR聚合算子的迭代算法应用问题。基于PULPR加性一致性和积性一致性，以及两个PULTS或PULPR之间的距离测度和相似性测度，可针对具体应用研究问题，设计迭代算法，开展决策对象聚类分析或对不同决策者的观点判断进行修正等，以提高群体意见的一致性水平，进而满足设定的阈值。

基于PULTS的多准则群决策理论与方法能够为模糊不确定环境下的群决策提供理论依据与技术支持，除以上提供的应用研究领域外，此类多准则群决策技术能够适时运用到“区域经济协调发展战略”“乡村振兴战略”“创新驱动发展战略”等国家重大战略决策的制定及协调区域融合发展中，并发挥辅助性作用。