1.工程项目群优选问题描述

大中型工程类企业（如与水利工程、土木建筑工程、海洋工程、城市改建工程、“菜篮子工程”等相关的企业）选择集群运作的项目群，往往是在企业战略规划的指引下，将具有交互耦合关联且多类型资源约束牵制的多个子项目构成项目群，同时将不同子项目组合构成的项目群作为“备选方案”。进行大中型工程项目群优选采用多准则决策理论与方法，假设多种项目群组成的备选方案集为；所构建的项目群优选评估指标体系中的各项指标可作为多准则决策中的准则，构成的准则集定义为；邀请咨询顾问、建设单位、施工单位、项目公司、供应商等项目群的实际参与者及研究人员组成专家组，参与项目群优选决策全过程。大中型工程项目群优选问题的实质是专家组通过构建的项目群优选评估指标体系，针对不同组合构成的项目群，采用多准则决策最终实现对备选项目群的优劣排序。

2.工程项目群优选评估指标体系构建

大中型工程类企业如何确保项目群中各个子项目的合理组合搭配，需要考虑项目群对企业当前发展阶段所制定企业战略的支持程度，即工程类企业的发展战略规划直接决定交互耦合关联的项目需要采用项目群的方式进行集群式管理运作。首先，合理化的项目群优选能使企业的各项资源以及资源的原始积累、开发等始终维持在一个较高的水平上。其次，在优选项目群运作的全生命周期，相关联企业的组织管理能力将得到明显提升，在长期实施项目群管理后，及时依据企业发展阶段修正或调整企业战略规划，以适应企业发展需求。此外，项目群中各子项目之间在资源分配、技术条件、市场需求、运作成本及收益等方面存在相互牵制和约束关系，需要在伦理气氛下从参与决策全过程的专家组及利益相关者的整体视角，确定项目群优选指标体系，从而确保所选定的项目群在组织层面、单个项目层面实现整体利益协同，达到经济效益和社会效益的综合价值最大化。最后，构建的项目群优选评估指标体系需要兼顾项目群的风险因素，使项目群的优选排序能尽可能地降低整体风险水平，相应的风险应对举措有利于项目群获取更高的综合效益。

基于上述分析，选取项目群对企业既定战略支持度、子项目间的关联性、项目群体风险水平、项目群综合效益这4个一级指标作为项目群优选评估指标，一级指标集记为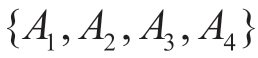。其中，A1包含战略目标匹配度（A11）、企业资源（A12）、组织管理能力（A13）、核心竞争力（A14）这4个二级指标，A2包含子项目间的效益目标相关性（A21）、资源规划和分配相关性（A22）、企业组织管理体制和运作机制相关性（A23）这3个二级指标，A3包含资源分配风险（A31）、组织管理风险（A32）、技术知识风险（A33）、财务风险（A34）、品牌风险（A35）这5个二级指标，A4包含投资利润率（A41）、内部收益率（A42）、经济净现值（A43）、经济内部收益率（A44）这4个二级指标。需要说明的是，针对不同类型的大中型工程类企业项目群，可对4个一级指标下共计16个二级指标进行具体解释，每个二级指标的含义和涵盖范围也可灵活调整。

3.工程项目群优选决策步骤

步骤1　根据大中型工程项目群评估指标体系，通过层次分析法（AHP法）确定各二级指标的权重。

首先，建立指标评价的量化等级表，由利益相关的各领域专家组成的评估小组对两层级评估指标的每一层进行两两比较，从而根据量化表原始等级构造同一层级指标的比较判断矩阵。4个一级评估指标两两比较得到判断矩阵B；在4个一级指标之下，分别得到各自的判断矩阵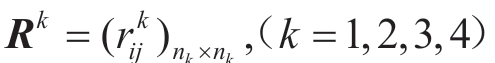，其中k表示相应的一级评估指标，nk表示一级指标所包含的二级指标数量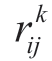，表示各二级指标两两之间相互比较的等级量化结果，即

其次，由判断矩阵B ，Rk计算各矩阵最大的特征值λmax及其特征向量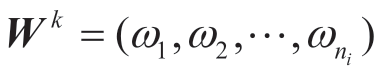，特征向量中各分量分别反映同一层级下各指标的相对重要程度，接着检验判断矩阵的一致性程度，计算一致性指标值C.I.：

最后，根据AHP法，通过平均随意一致性指标R.I.，计算随机一致性比率C.R.。当C.R.＜0.1时，相应的判断矩阵通过一致性检验，所求得的权重向量即为各指标之间相对重要程度的度量；当C.R.＞0.1时，需要专家组对判断矩阵中部分等级判断结果进行修正，直至通过一致性检验。将通过一致性检验的权重向量W k进行归一化处理，即

步骤2　确定针对每个二级评估指标的隶属度评价等级。一般地，评价等级数常取3到7之间的常数，由项目群优选评价的决策者得到各备选项目群关于各二级指标的模糊评价结果，从而在各指标下得到所有备选项目群的评价矩阵Tm，其中m为对应的二级指标。(www.daowen.com)

采用FCE与DEA相结合的评价方法，针对所有的备选项目群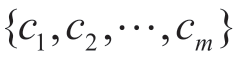，基于项目群选择优化与当前工程类企业发展战略高度一致的原则，选取各备选项目群针对某个二级评估指标的输入、输出变量，以效率评价指数≤1为约束条件，构建线性规划模型，确定各备选项目群对每个二级评估指标的隶属度，从而获取各备选项目群在所有二级指标下的隶属度矩阵，记为

步骤3　备选项目群在单个指标下的隶属度反映出该项目群在该指标下的优劣程度，再结合各二级项目群优选评估指标的权重，采用改进TOPSIS法获取所有备选项目群的优劣排序。首先，由隶属度矩阵确定正、负理想项目群隶属度向量，即

根据归一化后各二级指标权重，计算各备选项目群与正、负理想隶属度向量的加权距离，即

由于传统TOPSIS法中，与正理想隶属度向量加权距离最大的备选项目群，未必与负理想隶属度向量的加权距离达到最小。这里改进TOPSIS法，从备选项目群整体考虑，计算各备选项目群与正、负理想隶属度向量的相对加权距离，从而得到

步骤4　若充分考察所构建的项目群优选评估指标体系中所有一级指标及其相应的二级指标的差异性，由扩展VIKOR法根据所得各备案项目群的隶属度矩阵，可计算其效用值、个体遗憾值及综合评价值，从而获取最优项目群或折中备选项目群集合。

最后，计算各备选项目群的效用值和个体遗憾值的正理想解与负理想解，即

综合以上各备选项目群的效用值和个体遗憾值及正、负理想解，可得各备选项目群整体评价值：

其中ε为折衷系数，且ε∈[0，1]。若ε＞0.5，则倾向于使用最大化效用值进行项目群优选决策；若ε＜0.5，则倾向于使用最小化个体遗憾值进行决策；若ε=0.5，则通过协商达成一致的决策机制确定最优项目群。随着ε值的变化，决策者的主观偏好也在变化，所得到的排序结果会有一定的差异，更符合现实情境下的决策过程。

为获取备选项目群的优劣次序，分别根据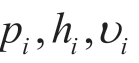对备选项目群排序，值越小对应的项目群就越优，从而得到关于所有备选项目群的3个排序结果。在整体评价值υi中，若最小值为υp，即对应项目群为cp，若同时满足以下两个条件，则项目群cp为最优化选择：（a）在对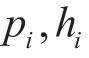的排序中，方案cp至少在其中一种排序中最优；（b）满足，其中υq为整体评价值υi排序中仅次于υp的取值，对应项目群为cq。当条件（a）不满足而条件（b）满足时，则折衷最优项目群为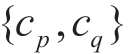；当条件（a）满足而条件（b）不满足时，解不等式，确定一个满足不等式且最大的υs，则折衷最优项目群为整体评价值介于υp与υs之间的所有项目群。

步骤5　综合考虑步骤3和步骤4所得备选项目群优选排序结果，审视伦理气氛下项目群优选决策的“有限理性”决策特征，以项目群优选保障项目群管理最终目标的协调一致性为导向，确定最终的项目群优化选择排序结果，大中型工程类企业可依据优选结果确定实际选择实施的项目群。