在潜艇研制方案遴选过程中，四位潜艇研究领域的专家需要从隐蔽机动能力（u1）、感知信息能力（u2）、武器装备攻击能力（u3）及防御能力（u4）这四个准则，对四个可实施研制方案进行评价。四项准则均为效益型准则，已知的专家权重向量W e=（1/4，1/4，1/4，1/4），即四位专家的地位是等同的，具备平等的话语权。四位决策专家采用的四个不同粒度的语言评价集分别为

关于不同粒度语言评价集中所包含语言短语的具体含义，这里不再赘述。四位决策专家针对四个可行性研制方案给出如下具有不确定语言变量评价信息的决策矩阵：

步骤3　针对决策者给出的四个不同粒度的不确定语言评价矩阵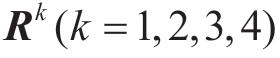，在每个决策专家下由式（2-18）计算任意两个方案之间关于每个准则比较的优势度，并由式（2-19）确定的各准则权重计算任意两方案之间两两比较的综合优势度，根据式（2-20）得到四个决策专家对应的综合优势度矩阵分别为

步骤4　根据已知的专家权重向量We，由式（2-21）得到群体综合优势度矩阵，即

由式（2-22）容易得到优于次数矩阵，即

由式（2-23）得到每个方案的总优先次数分别为a1=2.5，a2=0.5，a3=3.5，a4=1.5，根据总优先次数的大小得到方案排序结果为，即c3为最优实施方案，同时c1为次优方案，且方案c3优于c1的优势程度为0.541，据此可得相邻排序方案之间的优势程度。

为了将本节所给群决策方法与离差最大化确定准则权重的方法进行对比分析，首先针对潜艇研制方案遴选算例给出基于离差最大化及优势度的群决策过程，具体步骤如下。

步骤1　同投影及优势度的群决策方法的步骤1。

步骤2　根据转化后的区间二元语义决策矩阵，由离差最大化法计算单个决策者的准则权重向量。由转化后的具有不同粒度的区间二元语义决策矩阵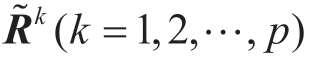，针对每个决策矩阵构建所有决策方案对所有准则评价偏差最大化的目标规划模型，即(www.daowen.com)

通过构造Lagrange函数求其最优解，并进行一致化处理，可得其最优解，即

步骤3～4　同投影及优势度群决策方法的步骤3～4。

下面利用该决策方法求解2.2.3节中的潜艇研制方案遴选实例。其中，步骤1与算例分析相同，以下从步骤2开始。将四个不同粒度的不确定语言评价矩阵Rk分别转化为区间二元语义矩阵形式，根据转化后的区间二元语义决策矩阵，由式（2-24）计算每个决策者对应的准则权重向量，分别为

在单个决策专家之下计算任意两个方案之间关于每个准则的优势度，由准则权重计算任意两方案之间的综合优势度，从而得到每个决策专家之下的综合优势度矩阵：

由专家权重向量W e得到群体综合优势度矩阵：

所得优于次数矩阵为

每个方案的总优先次数分别为a1=2.5，a2=0.5，a3=3.5，a4=1.5，根据总优先次数的大小得到方案排序结果为，确定c3为最优实施方案。

针对本算例，该群决策方法所得结果与基于投影及优势度的多准则群决策方法完全一致，验证了投影及优势度群决策方法的有效性。两种决策方法排序结果中相邻方案之间比较的优势度相差也不大，例如，2.2.3节中最优方案对次优方案的优势为0.514，本节决策方法最优方案对次优方案的优势为0.547。