1.决策问题描述

一般而言，每个决策者针对所有准则给出的权重信息是不完全的，要解决的多粒度不确定语言多准则群决策问题是在准则权重不完全已知的情形下，根据决策矩阵、决策者权重对各准则评价信息进行有效集结，并最终实现对方案的排序择优。

2.准则权重的确定

在转化的过程中，各方案准则值之间的相互关系保持不变，只有评价信息形式的改变，转换方法在理论上是完全合理的。

在准则权重信息不完全已知的情形下，准则权重的选择应当使各方案到正理想解的加权距离总和达到最小，同时与负理想解的加权距离总和达到最大。故可基于投影法确定各准则权重，即所确定的准则权重应当使各方案到正理想方案的加权投影值的总和达到最大，各方案到负理想方案的加权投影值的总和达到最小。由转化后的二元语义决策矩阵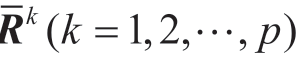可得决策者ek下的正、负理想方案的准则值向量分别为

3.群决策方法及步骤

对于不确定语言变量的准则评价值，虽然其具有一定的不确定性，但其本身涵盖了决策者所要表达的准确评价信息。由于各决策者评价所采用的语言评价集中的语言短语是均匀离散的，因此区间语言范围内的所有语言短语都等可能地覆盖了真实语言评价信息。不确定语言变量的概率密度函数可表示为

一般而言，经所有准则权重、决策者权重集结后得到的群体综合优势度矩阵应当满足弱传递性，若不满足，可根据文献[149]的方法调整矩阵P，使其具有弱传递性，否则会影响到群集结后方案排序结果的合理性。由群体综合优势度矩阵P构造优于次数矩阵A=（ail）m×m，其中(www.daowen.com)

由优于次数矩阵A的每行元素取值，可得方案ci优于其他所有方案的总优先次数，即

显然总优先次数ai越大，方案ci就越优，从而根据所有方案的总优先次数大小对各方案排序，而且由矩阵P可知方案排序结果中相邻位置上排序靠前方案对排序靠后方案的优势程度。

综上所述，基于投影及优势度的群集结及方案优选的步骤如下。

步骤1　决策者ek在Tk粒度下对决策方案ci关于准则uj进行测度，得到多粒度的不确定语言评价矩阵Rk，由式（2-13）将Rk转化为区间二元语义矩阵形式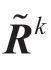，接着由式（2-11）、式（2-14）将区间二元语义决策矩阵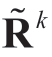转化为二元语义决策矩阵。

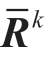步骤2　针对每个决策矩阵，由式（2-15）、式（2-16）计算其正、负理想方案的准则值向量，并由式（2-12）、式（2-17）计算单个决策者所确定的准则权重向量。

步骤3　在决策者ek下，由式（2-18）计算任意两个方案之间关于每个准则比较的优势度，并由式（2-19）计算任意两方案之间相互比较的综合准则优势度，根据式（2-20）得到综合优势度矩阵。

步骤4　由式（2-21）得到群体综合优势度矩阵，并判断矩阵的弱传递性，由式（2-22）得到优于次数矩阵，并根据式（2-23）得到每个方案的总优先次数，根据优先次数大小对方案排序。