针对具有语言评价信息的多准则群决策问题，早期的研究主要采用扩展原理或符号转移方法处理语言评价信息，所得评价结果往往不能用预先定义好的单个标准语言短语表示，难免会造成信息的丢失与扭曲，甚至出现与实际情形相悖的决策结论。为解决这一问题，Herrera提出了二元语义分析法，将语言短语评价信息转化为二元语义形式（集结运算结果也可转化为二元语义），基于二元语义集结算子或将二元语义与已有的多准则群决策方法相结合，集结决策者给出的针对各方案关于每个准则的评价信息，最终实现方案的排序择优。

由于所处领域不同，不同决策者会依据个人偏好采用不同粒度的语言评价集给出各自的语言评价信息，为对不同粒度语言评价信息进行统一处理，可在群集结过程中将语言评价信息转化为三角模糊数或由基本语言评价集表示的二元语义，从而实现对不同粒度语言评价信息的一致化。此外，在实际决策过程中，由于待决策问题的复杂性、不确定性以及不同决策专家知识水平、经验和对事物认知能力的差异，不同决策专家给出的评价信息为不同粒度下的不确定语言变量，此类评价信息充分考虑到决策者对事物认知的现实情况，并考虑到事物的不确定性与决策者的自身情况。针对不确定语言变量评价信息，文献[139-140]提出了多种不确定语言评价信息集成算子，并基于信息集成算子给出多准则群决策方法。文献[97]通过计算各决策者关于所有方案的优势可能度，并由OWA算子得到群体优势可能度矩阵，在模糊多数意义下获得每个方案的总体优势程度并对方案排序择优。

对于准则权重完全未知或不完全已知的情形，如何确定准则权重是集结评价信息的关键，Z.P.Fan[141]将不确定语言评价信息统一转化为梯形模糊数，基于传统TOPSIS法确定准则权重，给出一类多准则群决策方法。文献[93]在一致化多粒度不确定语言评价信息的基础上，通过构建所有方案与正理想方案的总贴近度最大化的目标规划模型确定准则权重，根据各方案与正理想解的贴近度大小得到排序结果；文献[35]基于相对熵确定准则权重，即所确定的准则权重应当使所有方案与正理想解的相对熵的和达到最小，同时与负理想解的相对熵的和达到最大，由不确定二元语义加权平均（UTWA）算子及有序加权平均（UTOWA）算子集结评价信息，得到所有方案的综合评价值；文献[91]构建基于离差最大化的目标规划模型确定准则权重，采用IT-WAA算子得到群体评价矩阵，根据两两方案之间比较的可能度矩阵及其排序向量获得方案排序结果。以上几个文献主要通过基本语言评价集对多粒度不确定语言评价信息进行一致化处理，分别采用TOPSIS法、离差最大化法、相对熵法等客观赋权法确定各准则权重，通过各种类型的信息集结算子、可能度矩阵或相对贴近度获得方案的优先序。

不同群决策方法的差异主要体现在信息集结及方案排序择优的方法上，这是决策方法的关键步骤，也是不同决策方法的创新性所在。由各方案的综合评价值构建的可能度矩阵会造成信息损失，而通过可能度矩阵的排序向量所确定的方案排序结果未考虑准则特征（效益型、成本型、折中型等）的差异，也会造成评价结果的偏差。TOPSIS法不能有效度量各方案与正、负理想方案的相对接近程度，对各方案优劣刻画不够精细，距离正理想解最近的方案未必距离负理想解最远，设方案A1到正理想解的距离小于到负理想解的距离，即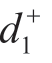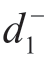＜，其贴近度大于0.5，若另一方案A2到正、负理想解的距离相等，即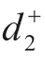=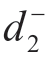，其贴近度为0.5，由TOPSIS法可知方案A1优于方案A2，而不用考虑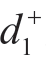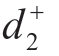，之间的大小关系，即使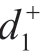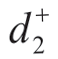＞，也就是说方案A1到正理想解的距离大于方案A2到正理想解的距离，但是会得到A1优于方案A2的结论，这显然是不合理的，这一点可看作TOPSIS法不够精细的一个层面。(www.daowen.com)

与TOPSIS法不同，基于折中优化的扩展多准则协调解（VIKOR）方法[142-143]能避免出现这一情况，在计算群效用值与个体遗憾值的基础上获得折中排序结果。目前，VIKOR法在不确定模糊评价信息的群决策问题中应用较多[144-146]，为多准则群决策问题中方案排序择优提供了新的思路。

鉴于以上分析，本节将扩展VIKOR法，引入准则权重完全未知的多粒度不确定语言多准则群决策问题，根据基本语言评价集将多粒度不确定语言变量转化为同一粒度，根据已知的决策者权重对各决策矩阵加权，得到群体决策矩阵，采用偏差最大化法确定各准则权重，由各方案的群效用值、个体遗憾值及综合评价值得到三种方案排序结果，根据折中原则得到各方案的最终排序结果。所给算例体现出该群决策方法的有效性和可行性。