不同空间权重矩阵的比较揭示了空间相互作用不仅取决于距离，还取决于各地区的经济状况。Moran I检验需要根据一定的空间结构，上节效应分析的空间模型需要事先确定模型结构（参数方法要在分析之前先验地确定相互作用的结构），而真实模型的结构是不知道的（McMillen，2010）。非参数方法承认真实模型结构的未知性，并可描绘空间依赖性和地理距离之间的灵活关系。在这里，用样条曲线相关图（spline correlogram）的非参数函数检验空间自相关（Bjørnstad，Falck，2001），并通过分解空间协方差来检验溢出效应（Conley，Ligon，2002）。如Yunlong Gong等（2014）用更灵活的非参数方法（样条曲线相关图）表现城市间房地产市场空间依赖关于距离的强度和半径，溢出效应非常显著，并在250公里的半径范围内下降。

非参数分析时SAR模型Y＝ρWY＋αlN＋Xβ＋ε，同样改写为：

Y＝(I－ρW)－1αlN＋(I－ρW)－1 Xβ＋(I－ρW)－1ε

该方程Y关于第k个解释变量的偏导表示为：

定义矩阵Sk（W）对角元素的平均值为直接效应，非对角线元素各行之和的平均值是间接效应。SDM模型的参数估计通过最大似然估计得到，唯一不同于SAR模型的是偏导矩阵：

地区i和j间随机场Z的空间自相关：

其中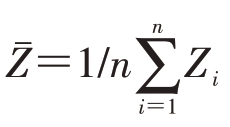，是样本均值。根据距离相关的自协方差非参数估计：

式中：K（.）——核函数；(www.daowen.com)

h（＞0）——带宽（调整拟合值平滑度的参数）；

dij——地区i和j之间的距离。

立方B样条（the cubic B-spline）的渐近核函数：

如果用方程（5.10）中的替代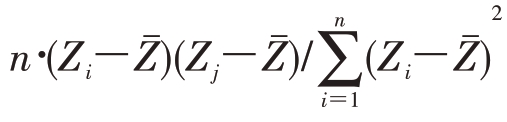，就得到样条相关图确定的空间自相关的非参数估计。yi表示地区i的制度，表示基于制度决定因素Xi和未知参数向量β的制度预测值。制度yi可改写为：

制度的空间自相关分解为三个部分：

方程（5.13）右边的第一项和第二项分别是可观测的空间协方差和不可观测的（残差）。第三项衡量地区j的可观察特征与地区i的部分制度（由地区i的可观测特征解释）之间的关系。因此，可表示空间溢出效应。这里的溢出效应被视为对协方差的衡量，而不是因果关系。