下面我们从经济活动聚集方式的变化—经济活动再聚集—的角度讨论经济功能区的形成过程。为了简化起见，这里仍然将所有区域分成两个空间区域，图1-4、图1-5将两个空间区域称作A地区和B地区，为了区别这里使用另外两个英文字母：和，即和表示由不同区位组成的两个区域。

（一）基本假定

第一，假定两个区域中的制造业包含n个产业（n≥3），每个产业i 生产无限量的品种差异υi∈[0 N]，，但每个品种只能由一个厂商生产，再进一步假定每个厂商只生产一个品种，一方面保证差异化的垄断竞争，另一方面是分析简化，这样产品品种就能和厂商一一对应。同样地，假定对所有产业来说品种差异上限均等于N。

第二，用A表示非熟练（技术）工人。有n类技术工人在特定制造业部门就业。一类产业对应一类工人，不失一般性，忽略第三产业，事实上分析结论可以很容易推广到第三产业。假定技术工人的种类也为N，产业i 仅要求一个i 类熟练工人（因而技术工人数量也为N）和ø数量非技术工人生产任意数量的某种产品。因此，生产某种产品的边际成本为0。

技术工人可以跨区域移动，但不可以跨产业移动，而非技术工人可以跨产业移动，但不能跨区域移动。前者很可能是因为一种技术工人通过训练获得的技术并不适应其他产业，当然这样假定还可以避免技术工人流向农业部门。现实中制造业经常跨区域分布，技术工人当然可以跨组合移动。后者的非技术工人既可在区域内从事农业活动，也可在组合内从事每类制造业生产。

i 类厂商在区域x 的数量可以记为λiN，在区域y？ 的数量则为（1- λi）N。

农业部门生产两种农产品（这样就打破了传统的农产品只有一类同质产品的假定），同时假定每种农产品只能由某个区域生产，可以记为农产品x 和农产品y。农产品x 只生长在x 区域，农产品y 只由y 生产，比如东北主产大豆，河北盛产棉花。该假设可以利用李嘉图比较优势理论证明。

前述假定可以实现我们的一些目的。第一，我们可以简单地用技术工人的种类区分产业，本部分的结论是再聚集均衡，也可由技术工人的聚集形态简单表示；第二，我们可以考察某一区域的农业就业份额；第三，经过简化处理，模型可解出明确结果。

（二）建立模型

每个区域的典型消费者的偏好可用下面的效用函数表示。其效用来自n种制造业产品qm、qa两种农产品和一种特殊产品qs。

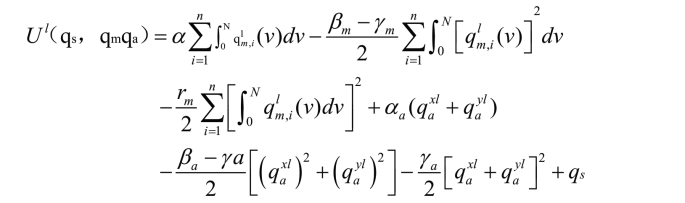
式中的参数α表示对某部门的喜爱程度，γ表示产品间的替代性，β-γ＞0表示喜爱产品的多样性，若β-γ趋近于0，则表示只有农产品一种，l表示区域。假定价格基准在两个区域相同，其边际效用也相同，不是一般性地将其标准化为1。

典型消费者的效用最大化的预算约束为：

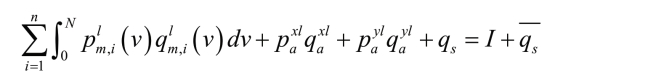
其中，I表示收入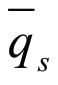，表示最初的环境清洁水平。令

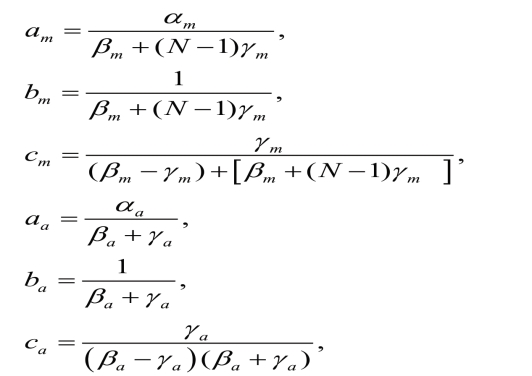
则消费者对制造业产品的需求函数为：

式中的工业品的价格指数

我们假定N充分大，这样单个厂商的价格变动不会影响价格指数，这也是垄断竞争的基本假设。由厂商追求最大化的利润，有

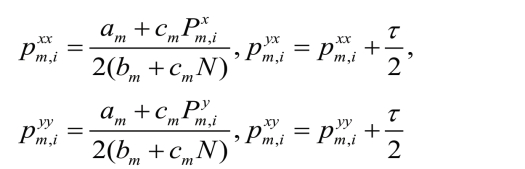
解之可得：

我们已经假定农产品生产是规模报酬不变的，且其价格由供求曲线交点决定。方n 便起见，进一步假定每n 个从事农业生产的非技术工人生产一个单位的产品。因为有的非技术工人在区域x（区域y）进入制造业就业，则有

若假定农产品运输成本为零，可以得到：

式中L=nN，是技术工人总量。产品价格确定以后，工业厂商的毛利润为：

由于市场结构是垄断竞争的格局，厂商数量众多，进入和退出是自由的，均衡的条件就是利润为零。(www.daowen.com)

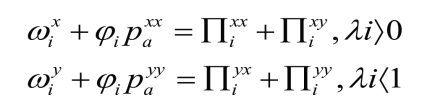
工资差异为：

由此得出区域l 的居民间接效用函数：

式中是除l 以外的区域。

（三）均衡分析

在均衡分析之前，我们再引入一些有用的参数：

其中，i ，j=1，2， …， n， i≠j 。

可以发现，ω 和µ不依赖于农业部门，后文会对这些参数进行解释，因为δij=δji，则矩阵Δk=（δij）k×k，（k=1，2，… n）是对称的。还有

再假定所有部门所有产品都会被消耗掉，在流动成本非常小的时候，对任何的λ，l，k，i，都会有。也就是当流动成本

第一个不等式来自于OTT（2002），这两个式子表示：第一，在每个区域的非技术工人相对于整个制造业部门来说足够多，或者两个区域的非技术工人的供给是无限的。这和刘易斯二元结构的假定相似，这是保证制造业能在任意一个区域聚集的必要条件，否则制造业在某个区域的聚集有可能会受到非技术工人数量的制约。第二，包含着的假定，也就是说消费者对农产品的偏好较为强烈。第三，可以得出，对于任意的τ〉0，µ〈0。两个区域的效用差为：

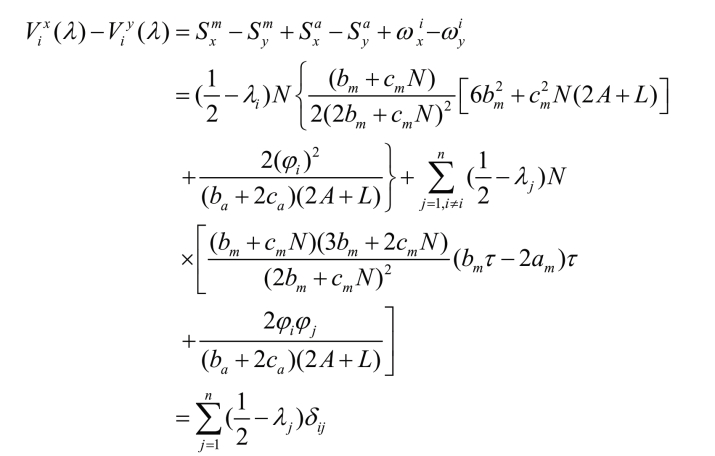
现在我们可以得出δij的解释了：

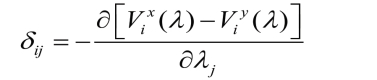
它表示一个j 类技术工人从x 到y 对不同的i类效用水平的影响。该影响包括对制造业部门和农业部门两部分的影响，分别为。对制造业部门来说，一个技术工人由x 移动到y，y 内产业j 的价格指数会发生变化，因为技术工人不会跨产业移动，j 类产业也会移动到y，显然这次移动对j 类产业的影响要大于对其他产业的影响。但是，对整个制造业的影响很小，因为流动成本非常小（τ →O）。相比之下，对农业部门的影响与τ 无关。

为了考察空间均衡的稳定性，我们使用经济地理学的传统假设：技术工人和厂商跨组合移动相对较慢，市场的调整是瞬时的。这就是说，工资调整远远快于劳动力的变化。劳动力的流动可以简单描述为：

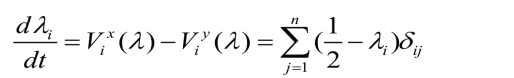
如果则（1/2，1/2，…，1/2）是上式的唯一内点均衡。因为是对称的，内点均衡稳定的条件就是：

下面我们就可以讨论均衡的稳定性了，均衡过程明显体现了流动成本τ 下降的全过程。不失一般性，我们假定产业1处于产业链的最前端，劳动密集性最高，而且φ1≥φ2≥…φn，其中至少一个不等式没有等号，且φ1〉0。

在任何稳定的均衡中，有，因此，对任意产业，如果i 产业和j 产业均聚集于 x （ i〈 j），则有，则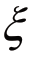产业也必然聚集于x。下面我们可以假定两个区域包含的区位刚好等于产业的个数n，这样，每个产业在各个区位之间的关系也同样遵循这样的规律，按照产业链的顺序和劳动密集程度分布。

对于不同的产业，总存在，（ i〈 j）。而且非技术工人成本在均衡中起到很重要的作用，它的高低要适宜支持产业在需要的区位集中。证明过程较为复杂，这里省去。

（四）再聚集过程

我们观察到，虽然各个区位的非技术工人的供给是无限的，但是需求量却是明显不同的。我们前文假定处在产业链最前端的产业也是劳动密集度最高的，这样如果各区位排成一条直线的话，对劳动力特别是非技术工人的需求呈现逐渐递减的趋势。如果是非线性排列的，对非技术工人的需求也会呈现十分规则的形状。所以这种情况对于各区位劳动力分布不均的一般非对称区域也是适用的，甚至这种非技术工人的空间分布状况对厂商的区位选择也会产生或大或小的影响。

如果流动成本τ 很小，两个及以上产业分散的均衡是不存在的，唯一的均衡是各个产业分别聚集的分离均衡。或者说，至多一个产业分散分布，其他产业则分别聚集于各个区位。此外，我们还发现了所谓的“门槛”产业，如果i 产业是区域l 的最小的产业（ λi），那么i 产业就成为该区域的门槛产业，如果有产业退出的话，最可能就是i 产业，而且只有大于i 产业的产业（ λρ）才可能聚集于区域l。

也就是说，随着经济主体为追求利益最大化而导致的区位选择的变化，会出现显著的经济活动空间分工，空间分工的结果就是相同或邻近的产业倾向于靠近分布，形成经济功能区。若简单地将聚集于各个产业所占据的空间称为经济功能区，根据前面的分析，在两个区域中就会出现 1-n或n 个经济功能区。