根据之前的设置，本书将使用房地产证券、股票以及无风险资产来构建投资组合，研究房地产证券下的投资组合动态配比策略、房地产证券资产在投资组合中的作用以及动态相关性对整个投资组合配比的影响等问题。在香港市场上，本书选取恒生房地产基金指数回报、恒生公共事业指数回报、Hibor隔夜利率来分别对这三种资产进行描述。为了在每一个时间点上构建最优投资组合，需要知道该时间点上三类投资标的预期收益率、预期波动率以及预期资产间相关性。如前所述，这里采用同Case等（2012）相同的设置，即将整个样本期内的预期收益率与预期波动率设置为常数值，只有资产间相关性动态变化。对于市场上的每一种资产而言，其常数收益率被设置为整个样本期内的回报平均值，即表5-1中第1行的值，而其常数波动率则设置为整个样本期内的标准差，即表5-1中第4行的值。然后本书针对每个市场上的三种资产回报序列，两两联合建立DCC-GARCH模型进行计算，得到三组动态相关性序列，再分别与对应两种资产回报的常数标准差相乘，即可得到投资组合计算时所需要的动态协方差序列。

表5-3　DCC-GARCH模型估计结果

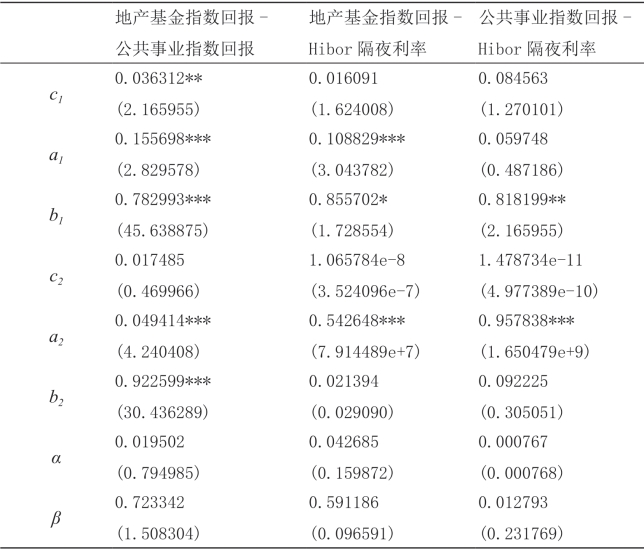
★表示p＜0.1，★★ 表示p ＜0.05，★★★ 表示p ＜0.01

表5-3给出了三个时间序列两两配对建模下的参数估计情况。估计值根据两步极大似然估计法得出，同时在括号中给出相应的t统计量结果，并标注t检验的显著性情况，从而判断模型得到的参数估计结果是否显著异于零。地产基金指数回报与公共事业指数回报联合建模时，地产基金指数回报波动率的常数项参数c1、ARCH效应参数a1与GARCH效应参数b1都具有很高的显著性，说明地产基金指数回报波动率变化的长短期效应都非常明显，公共事业指数回报波动率的ARCH效应参数a2与GARCH效应参数b2也具有很强的显著性，其长短期效应同样明显。而这两个指数回报序列分别与Hibor隔夜利率联合建模时，地产基金指数回报波动率的参数估计结果较为一致，公共事业指数回报波动率的ARCH效应参数a1不再具有显著性。Hibor隔夜利率在两个模型下的参数估计结果则均显示出很强的ARCH效应，参数估计在1%水平下显著，GARCH效应则不具备显著性。而在相关性参数方面，三组模型中的α与β都没有体现出一定的显著性，说明三组回报率序列间的相关性受到过去条件协方差以及过去单个指数回报波动性的影响都较为一般，但是从动态相关性的计算结果来看，整个相关性的结果仍然显示出时变的特征。

由于本章主要关注动态投资组合的配置，而根据之前的模型设置仅需要关注资产间的动态相关性情况，因此不再根据所得到的参数估计值以及模型设置计算各个序列的动态波动率，而是直接关注房地产基金指数回报、公共事业指数回报与Hibor隔夜利率之间的两两动态相关性。房地产基金指数回报与公共事业指数回报间的动态相关性在2010年4月20日达到最低点24.53%，在2011年8月8日达到最高点48.91%，随后在2013年5月31也达到了局部的高点48.61%，非常接近整个样本期内的最高点，在这段时间内该动态相关性的变化较快，变化范围不是太大，相关性的平均值为34.19%。相比较而言，房地产基金指数回报与Hibor隔夜利率之间动态相关性的变化幅度和变化范围更大，最小值为2011年8月10日的-44.08%，最大值为2013年5月13日的42.02%，在2013年5月31日该相关性非常接近于样本期内的最小值，为-43.51%，而这一日期与最大值出现的日期仅相隔13个交易日，且在整个样本期内动态相关性经历了多个局部高点，与最大值都非常接近，不过该动态相关性的平均值仅为3.49%。与前两者比较，公共事业指数回报与Hibor隔夜利率之间的动态相关性的变化范围明显小很多，局部的变化程度也更弱，最低点出现在2010年2月8日，为-3.67%，最高点则是2013年5月21日的5.04%，整个样本期内的动态相关性均值为2.21%，与两个极值点都相差不大。

图5-2　地产基金指数回报与公共事业指数回报的动态相关性

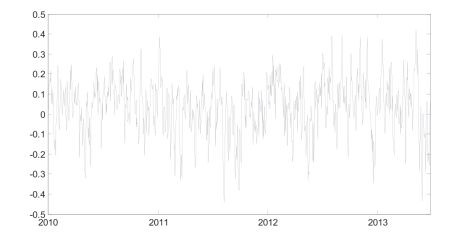
图5-3　地产基金指数回报与Hibor隔夜利率的动态相关性

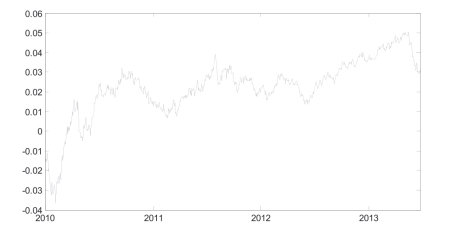
图5-4　公共事业指数回报与Hibor隔夜利率的动态相关性

在得到这三组动态相关性之后，基于常数预期收益率与常数预期波动率，就可以得到投资组合计算时所需要的动态协方差序列，从而进行投资组合的动态配置。最优组合方法中需要设定一个基准的组合方差，这里将一个总资产份额1/3为房地产基金指数、1/3为公共事业指数、1/3为无风险资产的固定投资组合作为参考投资组合，经计算这种投资组合在整个样本期内的方差为0.187814，本书将该值固定为最优动态投资组合一直保持的波动率水平，并以此计算出常数预期收益率、常数预期波动率下的最优投资组合动态配比情况，以及以常数预期收益率计算得出的最优动态投资组合日度收益率情况。(www.daowen.com)

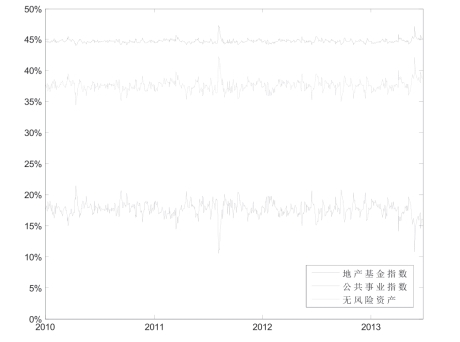
图5-5　动态投资组合配比情况

图5-5给出了在本书设置下投资组合中三种资产的动态配比情况。从图中可以看到三种资产的配比相对而言比较稳定，这是由于本书将每一日的预期收益率和预期波动率都设置为常数，且动态相关性逐日的变化较小的缘故。房地产基金指数在整个投资组合中始终占比最大，最大时点为2011年8月8日，占投资组合的47.24%，次高点为2013年5月31日，此时的地产基金指数占比为47.17%，两者相差非常之小，从图中可以看到地产基金指数占比最小的时间并不明显，数据显示2010年4月20日时的比率最低为44.05%，整个样本期内的占比平均值为44.75%，与最低占比更为接近。

无风险资产亦即Hibor隔夜利率的动态配比情况与房地产基金指数的动态配比在走势上非常接近，最高点也出现在2011年8月8日，占比大小为42.23%，，次高点也和地产基金指数动态占比的次高点一致，为2013年5月31日，占投资组合的42.13%，由于整体的占比波动叫地产基金指数更为明显一些，最低点在图中也较容易识别，同样出现在2010年4月20日，大小为34.48%，整个样本期内的平均占比达到37.60%。

由于地产基金指数和无风险资产的动态配比情况在走势以及高低点的出现时间上具有相当高的一致性，因此公共事业指数在整个投资组合中的动态配比情况就呈现出镜面的反向走势。实际上，公共事业指数也是在三种资产中整体占比最小的，整个样本期内的配比平均值仅为17.65%。动态配比最大值出现在2010年4月20日，为21.47%，最小值则在对应的2011年8月8日，该日占比10.53%，2013年5月31日也相应的成为公共事业指数动态配比的次低点，大小为10.70%。

值得注意的是，在动态配置中三个极值出现的日期，2010年4月20日、2011年8月8日、2013年5月31日正是房地产基金指数回报与公共事业指数回报间的动态相关性达到最低、最高、次高的日期。这说明在配置动态最优投资组合时，这两个指数回报间的动态相关性在三组动态相关性之中最为重要，影响最大。该动态相关性的趋势与房地产基金指数的动态配比趋势一致，而与公共事业指数的动态配置具有反向关系。通过对比三种资产的动态配置情况，可以发现房地产基金指数的动态配置波动性最弱，在资产组合中的比例变化最小。

得到最优投资组合的动态配比之后，可以使用三种资产每日的收益率配合各自的动态配比大小，计算得到该动态投资组合的日度收益率情况，图5-6分别给出了投资组合动态配比下的日度回报情况以及价值涨跌趋势。可以发现，不论是图5-6a中的日度回报，还是图5-6b中的价值走势，整体看来与房地产基金指数的回报、指数走势都非常接近，这一是由于房地产基金指数在投资组合中始终占比最高，二是源自于极端走势下房地产基金指数的动态配比的额外增大，特别是动态投资组合价值在2011年8、9月间的局部下跌非常明显的反映了这种接近的特征，实际上在这段时间内公用事业指数和Hibor隔夜利率的走势都较为稳定。

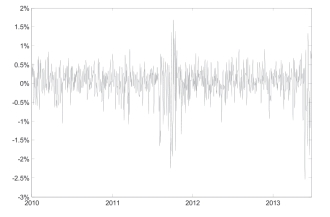
图5-6a　动态投资组合日度回报

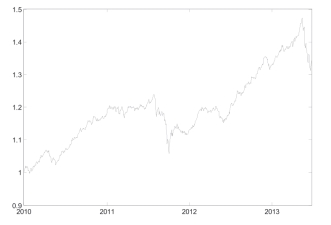
图5-6b　动态投资组合价值

为了同时说明动态相关性在投资组合中的作用，进一步引入最优固定投资组合作为对比，该投资组合与最优动态投资组合的唯一差别是资产间相关性被设定为常数，其具体大小如表5-2中所示，整个静态投资组合的方差仍然设定为总资产份额1/3为房地产基金指数、1/3为公共事业指数、1/3为无风险资产的参考投资组合的样本方差，即0.187814。通过优化可知，三种资产的固定占比分别为44.58%、18.31%、37.11%，相应的投资组合静态回报则为0.035216。而图5-5a中动态投资组合日度回报的平均值经计算为0.035296，较之固定投资组合的静态回报略大，这说明动态相关性在投资组合中存在着一定的优化作用，但是这种优化作用在本章研究中显著性不高，这主要是源自于日度数据下动态相关性变动的相对缓慢，以及固定预期波动率和预期收益率所带来的对现实情况描述的弱化。