在上一章的研究中，使用了DCC-GARCH模型来研究香港房地产市场和股票市场时间的动态相关性。这一章则将尝试使用VAR-DSTCC-GARCH模型来研究不同地区房地产市场之间的动态相关关系。DSTCC-GARCH模型也同DCCGARCH一样，具有将序列间相关性刻画为时变的能力，放松了资产间的相关性在全部研究时间内都保持不变的假设，有能力表述市场上新信息的不断冲击等现实情况。在此基础上，该模型还进一步细化了时变相关性的动态过程，允许该相关性受到两个外部因素的影响，从而优化了模型的刻画能力。

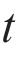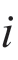在本章研究的框架中，首先使用一个VAR模型来刻画多个不同地区房地产市场之间的回报驱动关系。假设在某时间点，观测到第个地区房地产资产对上一个时间点的回报率为。VAR（p）的模型结构可以表述为：

其中k表示参与VAR模型建模的时间序列数量（在本章研究中为4，表示4个不同地区的房地产市场），而p则表示VAR模型中解释变量的滞后阶数，和为VAR模型参数，为模型残差。为一列均值为0方差为1且相互独立的随机变量，Ft是时间点t下的信息集。

在经过VAR模型处理得到对应各个序列的残差之后，使用DSTCCGARCH（1，1）模型来处理各个市场间的动态相关性，本书将分别两两配对地区市场并进行DSTCC-GARCH模型的建模，因此设置i为1和2。为表述方便，记，。设两个VAR模型残差序列的方差协方差矩阵为Ht，则Ht可表示为。再设两个残差序列的条件相关性矩阵为Vt，Vt可以表示为。根据前面的设置，Ht与Vt的关系为：

其中

当Vt不随时间变化，即，动态条件相关性将退化为常数条件相关性。相应的，DSTCC-GARCH模型将退化为CCC-GARCH模型。

记矩阵Ht中各项分别为Hij，t，矩阵Vt中各项分别为ρij，t。则它们之间的关系可以表述为：

首先针对模型的波动率部分进行设置，本书使用GARCH（1，1）建立模型：(www.daowen.com)

其中为截距项，ai表示冲击对方差的短期影响程度（即ARCH效应），bi表示冲击对方差的长期影响程度（即GARCH效应）。ai和bi之和应当小于1，从而保证模型的稳定性。

由于建模时采用两两配对的形式，因此式（3.6）中的时变相关性ρij，t可以简记为ρt，即Vt非对角线上的两个元素是一致的。其时变相关性结构可以由如下式子进行描述：

其中逻辑项Gjt为转换项，Sjt为转换变量，可以是随机的或者确定的。系数γj决定了转换的速度，其可以为正值或者负值，这样Sjt就可以基于不同方向影响转换行为。系数cj决定了转换发生的位置。相关性ρt是四个正值的结合，ρ（11）、ρ（12）、ρ（21）和ρ（22），其中每一个都表示一种常数相关性的极限状态。对这四个极限值的限制为，因此DSTCC-GARCH模型中的动态条件相关性就可以表示为：

观察值的对数似然函数如下

通过最大化L可以得到参数的估计值。

为了增加估计过程的数值精确性，首先将参数分为三组： GARCH组，相关性组，转换组，并反复的循环，针对其中一组进行似然函数的寻优。似然函数每一次将其他组的参数固定为之前所得到的估计值，针对其中一组参数被最大化。当某一次新的估计结果不能将整个似然函数提升超过一个固定的阈值程度时，就可以停止循环估计过程，得到一个收敛的结果。