对于n维向量随机过程

其中，Yt=（Y1t，…，Ynt）＇，Ai表示n×n阶的系数矩阵，ui~iidN（0，∑u）为不可观测的零均值独立白噪声过程，并且其协方差矩阵为非时变正定矩阵。

如果n维向量随机过程Yt是平稳的，则式（6.1）被称为VAR模型。如果Yt中部分或者全部随机过程是I（1）过程，而且它们存在协整关系，则式（6.1）可以表示为VECM模型

其中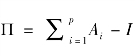，被称为长期关系矩阵，，（i=1，2，…，p）是短期参数。

这时，由于Yt中存在协整关系，矩阵Π是奇异矩阵，假设Π的秩为r，则存在秩为r的n×r阶矩阵α和β，使得Π=αβ＇；并且，Yt中存在r个线性独立的协整关系。其中，载荷矩阵α代表了变量间长期均衡的调整方向和速度；β是协整向量的矩阵，反映了经济变量之间的长期均衡关系。

因此，由格兰杰表示定理的Beveridge-Nelson MA表示（Johansen，1995）可知，如果Yt是由VECM模型

生成，则存在如下的VMA表示

以下为估计系数矩阵的步骤：

由式（6.3）可得，

于是，系数矩阵可从估计平稳VMA模型（6.3’）得到。

首先，假设平稳VAR模型

的VMA模型表示为(www.daowen.com)

则^[1]

从而，得到VMA模型系数矩阵的计算过程

于是，估计平稳VAR模型后，对比式（6.3’）可得

因此，系数矩阵的估计如下：

对式（6.2）左乘一个结构矩阵A，即可转化为SVEC模型

其中，Aut=Bεt，B是n×n阶矩阵，εt是n×1阶均值为零相互正交的结构冲击向量。

于是，当A可逆时，

并且，由Beveridge-Nelson的VMA表示可知，Yt具有结构向量移动平均（SVMA）表示

其中，A和B均为非奇异矩阵，ΞA-1B仍然是秩为n-r的矩阵。

而且，相应平稳VAR模型的SVMA模型为