最早由Sims（1986）提出并运用于宏观经济政策分析。基于经济理论建立的SVAR模型不仅能够反映经济变量之间的同期结构性关系，而且也揭示了经济变量间的动态关联。因此，SVAR模型弥补了向量自回归模型（VAR模型）缺乏经济理论基础，不能反映经济结构的不足。递归假设识别方法、长期约束识别方法和符号限制识别方法均是通过对结构VAR模型施加内部约束条件进行识别与估计的，下文将介绍新的识别与估计结构冲击的方法，即利用模型之外的工具变量来识别结构冲击的方法SVAR-IV。

传统的SVAR模型识别方法是基于理论基础和经济意义对其结构参数矩阵直接施加内部约束条件或是对模型中变量施加符号限制，但是在研究实际问题的过程中，模型中的变量会受到市场经济运行环境和宏观调控机制渐进式变化的影响，而这些变化又无法被准确量化，不能加以控制使模型中解释变量和被解释变量免受其影响，从而被遗漏在误差项中，导致模型出现内生性问题（杨继生，2019）。为解决这一问题，目前，越来越多的经济学家开始运用外部工具变量的方法来识别宏观经济冲击的动态因果效应，即“SVAR-IV”方法。这是一种将外部序列纳入识别的新方法，利用VAR模型之外的信息来识别结构冲击。国外学者Stock&Watson（2008）最先对其进行阐述，并且Stock&Watson（2012）以及Mertens&Ravn（2013）对其进行扩展。

Stock&Watson（2018）指出外部工具的使用开启了宏观经济中一个新的研究领域，在这个领域中，利用与宏观经济政策冲击相关的但独立于模型之外的外部工具的随机变化来获得可靠的识别。虽然在许多应用情形中，通过对政策冲击的部分衡量来构建工具变量，作为真实冲击的代理变量会产生偏差，但是这种工具变量仍然具有有效性。然而，类似于微观计量经济学中，这样的工具变量也是不容易得到的。尽管SVAR-IV方法存在缺陷，但是，Stock&Watson（2018）认为对SVAR模型进行识别时，运用工具变量的外部识别方法仍然比对SVAR模型施加内部约束条件的识别方法更可靠。

下文首先对动态因果效应进行阐述并介绍SVAR模型转化为结构移动平均（SMA）的过程；然后，介绍利用外部工具变量识别与估计SVAR模型的新方法；最后，说明SVAR-IV方法成立的必要条件，即可逆性的问题。

（1）动态因果效应与结构移动平均过程

对于宏观经济系统，令ε1，tε1，t表示t时刻均值为0的随机指派的处理（ε1，t=0表示t期试验未发生，ε1，t=1ε1，t=1表示t期试验发生），那么，在h期后，ε1ε1的单位冲击对变量Y2 Y2的因果效应可以表示为：

于是，在线性性和变量Y2 Y2平稳的假设下，则在h期后的平均处理效应是回归方程

的总体系数θh，21。

因为ε1，t是随机指派的，即在式（5.47）中，E（ut+h|ε1，t）=0，所以可知θh，21=E（Y2，t+h|ε1，t=1）-E（Y2，t+h|ε1，t=0）Θh，21=E（Y2，t+h|ε1，t=1）-E（Y2，t+h|ε1，t=0），因此θh，21表示结构冲击1对变量Y2在t+h期的因果效应。如果ε1，t可以观测，那么式（5.47）中的因果效应就可以通过OLS估计方法获得。因此，在不同时期（h=0，1，2，…）的θh，21组成的因果关系路径就是结构冲击1对变量Y2的动态因果效应。

在宏观经济中，随机处理ε1，t是指结构冲击，是一个原始的、非预期的经济力量或推动力，它是不可预测的并且与其他冲击无关。因此，在宏观经济学中，结构冲击是随机处理变量，而脉冲响应函数就是处理变量随着时间变化对相应宏观经济变量的动态因果效应。Slutzky-Frisch范式呈现了可观测宏观经济变量的路径，是由当前和过去的结构冲击和测量误差引起的路径。如果将所有这些结构冲击和测量误差集中在m×1维向量εt中，n×1维的宏观经济向量Yt可以用当前和过去的结构冲击εt表示，即：

其中，L是滞后算子，θ（L）=θ0+θ1 L+θ2 L2+...，这里θh（h=1，2，...）是n×m维系数矩阵。为了排除非重要的无关冲击，假设冲击方差矩阵是正定的。并且假设这些冲击相互独立，Ramey（2016）认为这一假设既符合其作为随机指派处理的要求，也符合他们作为原始经济力量的解释。其中，Yt Yt是二阶矩平稳的时间序列向量。

假设包含在结构冲击εtεt中的任何测量误差都与结构冲击无关，且ε1，tε1，t与其他冲击和任何测量误差都不相关，所以因果效应可以表示为：

显然，式（5.49）的平均因果效应等同于宏观经济学文献中经典的因果效应，即保持其他冲击不变，因果效应为偏导数∂Y2，t+h/∂ε1，t∂Y2，t+h/∂ε1，t。

式（5.48）也称为Yt Yt的结构移动平均表达式（SMA），θ（L）Θ（L）的系数既是结构脉冲响应函数，也是结构冲击的动态因果效应。自Sims（1980）提出SVAR模型以来，在宏观经济学中，估计结构移动平均（SMA）式（5.48）的标准方法是先估计结构向量自回归（SVAR），然后将SVAR模型转化SMA模型，再估计θ（L）。这一方法起源于Cowles委员会提出的时间序列变量联立方程模型的建模。这种方法有多个优点：宏观经济学家通常对多重冲击的反应感兴趣，而SVAR方法正好提供了对所有冲击的反应系数估计；并且，该方法通过对高维移动平均模型施加参数约束可以提高估计效率；特别，该方法用OLS估计单方程解决了多变量移动平均模型估计的计算难题。

当然，这些优点的成立有两个条件。第一个条件是须识别VAR新息和结构冲击之间的关系，即解决SVAR模型的识别问题；第二个条件是假设VAR新息和结构冲击张成相同空间，即可逆性条件成立。随后，本文就如何使用工具变量方法来解决这个棘手的SVAR识别问题进行理论分析。

（2）SVAR-IV识别

设向量自回归模型A（L）Yt=ut，将Yt Yt表示为其对过去值的投影加上一个新息ut ut，且该新息ut ut不能由Yt Yt的过去值线性预测，其中A（L）=1-A1 L-A2 L2-…，新息ut ut具有非奇异协方差矩阵。由于ut=Yt-Pr oj（Yt|Yt-1，Yt-2，...）ut=Yt-Proj（Yt|Yt-1，Yt-2，…），所以这种新息ut又被称为Wold误差。

在结构VAR模型中，假设新息是冲击的线性组合，并且假设新息所张成的空间与结构冲击张成的空间重合，即

其中，θ0是非奇异的。上式（5.50）成立的一个必要条件是VAR模型中的变量数等于冲击个数。又因为Yt是二阶矩平稳的，所以式A（L）Yt=ut中A（L）A（L）是可逆的。因此，从A（L）Yt=ut和（5.50）可以得出结构性冲击的移动平均表示，即

其中，C（L）=A（L）-1 C（L）=A（L）-1。

若（5.50）成立，则SVAR模型的脉冲响应函数揭示了总体动态因果效应，即C（L）θ0=θ（L）C（L）Θ0=Θ（L）。因此，条件（5.50）是结构移动平均模型满足可逆性的隐含条件。支撑SVAR模型分析的可逆性假设非常重要，将在下一小节详细讨论。

在可逆性假设下，SVAR模型的识别问题就是识别θ0Θ0。在此，本文总结了利用外部工具识别SVAR模型结构冲击的方法。

假设存在工具变量Zt Zt满足以下条件：

E（）=α＇=（相关性）

E（）==0（外生于其他当期冲击）

从上述两个条件和式（5.51）可以推导出：

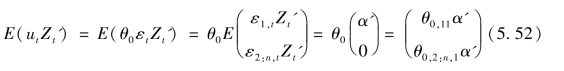
一般地，假设1个单位的ε1，tε1，t冲击使得Y1，t Y1，t变动1个单位，即θ0，11=1Θ0，11=1，称为单位效应归一化。借助于单位效应归一化，当工具变量Zt Zt为标量时，根据（5.52）可以得到

当拓展为多个工具变量时，Θ0，i1Θ0，i1就是使用工具变量Zt Zt进行估计的总体参数的估计值，即

由于新息ut ut是不可观测的，因此IV回归模型（5.54）是不可行的。一种可能的解决方法是用对应的样本拟合值（VAR的残差）代替式（5.54）中的总体新息u1，t。然而，虽然这样做将为强工具变量提供一个一致估计量，但由于是生成的回归量，Zt Zt和Yt Yt的滞后值之间存在潜在的相关性，因此必须调整θ0，i1Θ0，i1的标准误差。此外，θ0，i1Θ0，i1还可以通过直接产生正确的大样本、强工具标准误差的方法进行估计。因为ui，t=yi，t-Pr oj（Yi，t|Yt-1，Yt-2，...）ui，t=Yi，t-Proj（Yi，t|Yt-1，Yt-2，…），等式（5.54）可以重新写为：

其中，γi（L）γi（L）是Pr oj（Yi，t-θ0，i1 Y1，t|Yt-1，Yt-2，...）Proj（Yi，t-Θ0，i1 Y1，t|Yt-1，Yt-2，…）的系数。系数Θ0，i1Θ0，i1和γi（L）γi（L）可通过使用工具变量Zt Zt的两阶段最小二乘法进行估计。根据Zellner&Theil（1962）以及Zellner（1962）的经典结论可知这种两阶段最小二乘法估计不存在有效性损失，它实际上等同于三阶段最小二乘的系统估计方法。

因此，总结得到SVAR-IV估计的步骤如下：

第一，对Yt中的变量使用工具Zt估计模型（5.55），其中，Yt的p期滞后作为控制变量。与单位效应归一化Θ0，11=1一起，产生了Θ0第一列的IV IV估计值。

第二，估计一个VAR（p）过程并反解VAR模型，得到=。

第三，估计冲击1对向量Y的动态因果效应

其中，是滞后算子多项式的h期滞后算子系数矩阵的第i行向量。

动态因果效应估计量与工具变量的选取有直接关系，当工具变量IV与结构冲击强相关时，动态因果效应估计结果是可靠的；当工具变量IV与结构冲击弱相关时，动态因果效应估计结果受到一定的影响。对于工具变量合理性的解释，通常是估计政策变量关于工具变量的一阶段回归的F统计量。然而，目前存在一种异方差自相关稳健方法（HAR）用于检测弱工具变量并可在线性回归中对弱工具进行稳健性推断。如Andrews（2017）就提出了用于检测弱工具的一阶段F统计量的HAR替代方法。如果VAR模型中Y是可逆的，并且工具变量与控制变量不相关，那么HAR检测方法就不是必需的。此外，如果误差是同方差的，那么就可以运用同方差截面数据中弱工具识别方法，包括第一阶段F统计量进行检验。

（3）可逆性与遗漏变量偏差

显然，SVAR-IV方法可以得到有效结果的前提条件是结构参数矩阵θ（L）可逆，且此时工具变量是强工具变量。下面主要介绍可逆性的检验。

如果结构冲击εt能够εt能够由Yt Yt的当前值和滞后值来表示，即εtεt可以写为

那么SVAR模型中的结构参数矩阵θ（L）是可逆的。因此，式（5.57）被称为可逆性条件。

可逆性条件也是条件（5.50）ut=θ0εt ut=Θ0εt成立的必要条件。也就是说，若可逆性条件成立，则Θ0Θ0是可逆的，这是由于：

其中，式（5.58）中第二个等式显示当前和过去的新息张成了变量Y的当前和过去的空间，第三个等式和第五个等式都是由ut=Θ0εt ut=Θ0εt得到的，第四个等式表明εtεt是序列无关的。由于εt=Proj（εt|ut）εt=Proj（εt|ut），方程ut=Θ0εt ut=Θ0εt必须有εtεt的唯一解，因此Θ0Θ0的秩等于结构冲击εtεt的个数。而且，由于Var（ut）被假定为满秩，因此结构冲击εtεt的个数又等于SVAR模型中变量的个数，都等于Θ0Θ0的秩，即可说明Θ0Θ0是可逆的。

另外，可逆性条件成立也意味着在VAR模型中不存在遗漏变量（Fernandez-Villaverde et al.，2007），这是由于可逆性条件成立意味着结构冲击εtεt和新息ut ut张成了相同的空间，增加过去的冲击对VAR模型中的变量Yt Yt没有预测能力。也就是说，从可逆性条件可以得到

式（5.59）既说明了可逆性假设是很强的，又将可逆性解释为一个遗漏变量的问题。如果可逆性成立，那么真实冲击的历史不会改善使用VAR模型进行预测的结果。相反，如果预测结果通过在回归中加入历史冲击而得到改善，那么VAR模型就遗漏了一些变量。因此，VAR模型存在遗漏变量问题就表明违背了可逆性假设。

显然，可逆性是一种非常强的假设，在可逆性下，增加真实宏观经济冲击对于VAR模型的预测没有任何价值。并且，Forni和Gambetti（2014）指出可利用Granger非因果性检验推断可逆性。基于SMA模型的LP-IV估计和SVAR-IV估计，Stock&Watson（2018）给出了一种推断可逆性条件的Hausman型检验。

（4）案例：我国财政科技支出政策的宏观经济动态效应分析

中国的经济运行是政府监管和市场自我调节相互配合的，在经济结构偏离既定目标时可以通过运用宏观经济政策对宏观经济进行有效调控，最终实现宏观经济的基本目标：促进经济适度增长、增加就业、物价稳定和国际收支平衡。财政政策对宏观经济具有“内在稳定器”的调控作用，而政府财政科技支出政策作为财政支出政策的一个重要组成部分，是政府支持技术进步的着力点，必然对宏观经济增长、就业、价格水平和净出口等关键经济变量产生重要的影响。

高泽铭（2020）运用SVAR-IV方法识别和估计有关政府财政科技支出政策的动态因果效应。研究发现，财政科技支出政策在促进经济增长以及拉动净出口发展等方面存在显著的动态因果效应。但是，财政科技支出政策并未发挥出抑制通货膨胀的动态因果效应；而且该政策也是一把“双刃剑”，并不具有稳定就业的动态因果效应，对就业带来了双重“创造性破坏”的负面影响。最后，根据实证分析结论对中国财政科技支出政策的宏观调控能力进行评价，并得出了一些针对性的政策参考。

①变量的选取与数据的处理

变量的选取。

财政科技支出政策方面，国家通过增加或者减少财政科技支出达到刺激经济增长或者熨平经济波动的效果。本书从狭义的财政科技支出政策角度出发选取季度财政科技支出作为观测变量（用ST表示）。在2007年之前，财政科技支出用国家财政总支出项目中的国家财政科技拨款项目来表示，在2007年之后，财政科技支出用财政主要支出项目中的国家财政科学技术支出项目来表示，并将月度数据换算为季度数据。

经济增长方面，国家的产出增长率能够反映本国的经济增长速度。衡量产出增长率的指标有很多，包括工业增加值增长率、国内生产总值增长率等。国内生产总值反映了一个国家的经济活动所生产出的全部最终产品和服务的价值，学术界公认为衡量一国经济水平的最佳指标。该指标不仅可反映一个国家的经济状况，还可以反映一国的综合竞争力。本文参考刘金全和张龙（2018）的做法，选取季度国内生产总值作为测算经济增长的变量（用GDP表示）。

就业方面，借鉴王阳和牟俊霖（2018）的处理方法用劳动力总量反映一国的劳动力就业情况。由于季度劳动力总量数据的欠缺，并且在一年内每个季度的劳动力总量差别不是很大，因此选取年度劳动力总量数据作为当年每个季度的劳动力数据，即为反映季度就业情况的指标（用L表示）。

物价变动方面，学术界通常用物价指数的变动来衡量物价变动，常用的物价指数也有很多，包括居民消费者价格指数、国内生产总值平减指数、生产者物价指数等。张龙和金春雨（2018）指出在政策制定过程中，由于消费者价格指数的涨落影响居民的实际生活状况，因此政策制定者最为关注这一指标。本书借鉴其处理方法将消费者价格指数季度数据作为衡量物价变动的指标（用CPI表示）。

国际贸易方面，净出口是指商品出口及进口之间的差额，是一个国家收支差额中最大的组成项目，在国际贸易核算中的地位极其重要，而且数据易于收集，再加上国际贸易核算中其他项目差额受本文财政科技支出政策的影响不大，因此，本书选取季度净出口变量作为衡量国际贸易增长的代理变量（用NX表示）。

工具变量的选择。

为了有效地识别与估计政策结构冲击对宏观经济的影响，需要为政策变量寻找合适的外部“工具变量”。该“工具变量”需要满足两方面的条件，其一是满足“相关性”条件，即“工具变量”与政策变量高度相关；其二是满足“外生性”条件，即“工具变量”不影响模型中其他变量，来源于系统之外。因此，本书选取的财政科技支出政策的外部工具变量不仅要能够解释财政科技支出增长率的变动，还必须符合外生性的要求。也就是说，选取的外部工具变量有且只有通过财政科技支出政策间接影响经济效益，而不能通过其他途径直接或间接地对宏观经济产生影响。

在“工具变量”的选取方法中，Acemoglu等（2001）开创性地提出了滞后变量可以作为当期变量的工具变量的策略。根据这一思路，一个国家历史上的财政科技支出政策变化情况是路径依赖的，与从事科技活动机构数高度相关，同时，从事科技活动机构数与其他宏观经济变量的相关性微乎其微。因此，本书参考马光荣和李力行（2014）、赵曼和王玺玮（2017）、贾俊生等（2017）的做法，选取历年我国从事科技活动机构数作为财政科技支出政策冲击的外部工具变量，记为变量Z表示。通过查阅中华人民共和国科学技术部相关文件，1991年至2018年我国从事科技活动机构主要包括科学研究与开发机构、规模以上工业企业属技术开发机构以及高等院校属研究与发展机构三大部分，这三部分机构数的总和占我国从事科技活动机构数的绝大部分，因此，本书选取这三部分机构数之和作为我国从事科技活动机构数的代理变量。虽然《中国科技统计年鉴》以及中华人民共和国科学技术部相关文件只公布了1991年至2018年三部分机构数的年度数据，但是考虑到一年中各季度之间从事科技活动机构数相差并不大的事实，因此，本书选择1991年至2018年历年年度数据将其等值填充于相应年份各季度之中，得到1991年第一季度至2018年第四季度从事科技活动机构数的季度数据，并将其作为财政科技支出政策冲击的工具变量。

在对工具变量进行数据预处理的过程中，首先依据Census X-12季节调整法进行季节调整以消除季节因素的影响；然后对工具变量数据进行了对数化处理以减少异方差的影响，最后对其进行平稳性检验。单位根结果显示我国从事科技活动机构数Z的原序列ADF检验值大于5%显著性水平上的临界值，原序列是非平稳时间序列，而在对数化后的原序列进行一阶差分后，得到我国从事科技活动机构数增长率rZ的ADF检测值小于5%显著性水平上临界值，拒绝零假设，即rZ是平稳时间序列。

为了检验工具变量的外生性，借鉴方颖和赵扬（2011）的方法，本书对于宏观经济变量国内生产总值增长率、劳动力总量增长率、消费者价格增长率以及净出口，依次关于财政科技支出政策和工具变量（从事科技活动机构数增长率）建立回归模型，如果工具变量仅通过财政科技支出政策间接影响宏观经济变量，那么在控制财政科技支出政策的回归方程中，工具变量应该对宏观经济变量不显著。如表5.6最后一列结果所示，国内生产总值增长率、劳动力总量增长率、消费者价格增长率、净出口分别对工具变量的回归系数均不显著，而财政科技支出政策的回归系数仍然显著。如表5.6第二列和第三列结果所示，当宏观经济变量国内生产总值增长率、劳动力总量增长率、消费者价格增长率、净出口分别对财政科技支出政策和从事科技活动机构数增长率进行回归时，回归系数均显著。因此，工具变量并不直接影响宏观经济变量国内生产总值增长率、劳动力总量增长率、消费者价格增长率、净出口，而仅仅通过财政科技支出政策影响宏观经济变量。

表5.6　工具变量的外生性检验

数据说明。

本书选择1991年第一季度到2018年第四季度的时间序列数据，数据来源于《中国统计年鉴》《中经网统计库》《中国科技统计年鉴》《Wind数据库》。需要做出说明的是，本书除净出口NX外其他数据都采用季度环比增长率，用rST表示政府财政科技支出的增长率，用rGDP表示国内生产总值的增长率，用rCPI表示消费者价格增长率，用rL表示劳动力总量增长率。另外，本书所使用的数据都转换为以1990年第一季度为基期，并使用Census X-12季节调整法对所有原始季度数据进行了季节调整以消除季节性影响。

②构建SVAR模型

单位根检验。

为增强变量的稳定性，先对除净出口NX外的国内生产总值GDP、劳动力总量L、消费者价格指数CPI、以及财政科技支出ST各个变量的原始数据分别进行对数化处理。在对数据进行对数化处理的预处理之后，采用ADF检验对对数化后的四个变量与原始净出口变量进行单位根检验。检验结果如表5.7所示：(www.daowen.com)

表5.7　单位根检验

注：检验的类型C表示只有常数项。临界值是在5%的显著性水平下取得。***表示在1%的显著性水平下显著，**表示在5%的显著性水平下显著，*表示在10%的显著性水平下显著。

从检验结果中可以看出净出口NX原序列的ADF检验值小于5%显著性水平上的临界值，拒绝零假设，净出口NX是平稳时间序列。对数化后的国内生产总值GDP、劳动力总量L、消费者价格指数CPI以及财政科技支出ST原序列的ADF检测值都大于在5%显著性水平上的临界值，所以四个对数化后变量的原序列均是非平稳时间序列。而对这些对数化后的变量进行一阶差分后，得到国内生产总值增长率rGDP、劳动力总量增长率rL、消费者价格增长率rCPI以及财政科技支出增长率rST各序列的ADF检测值均小于5%显著性水平的临界值，所以拒绝零假设，即rGDP、rL、rCPI以及rST都是平稳时间序列。

Granger非因果关系检验。

上述平稳性检验的结果说明变量之间存在稳定的长期关系，但是不能说明变量之间的因果关系。为探究和确定变量之间关系，本书进一步进行Granger非因果关系检验，以考察各经济变量与财政科技支出政策之间的Granger非因果关系。检验结果如表5.8所示。

表5.8　Granger非因果关系检验结果

上述Granger非因果关系检验结果解释如下：

第一，财政科技支出增长率（rST）与国内生产总值增长率（rGDP）之间存在双向的Ganger因果关系。财政科技支出增长率（rST）是国内生产总值增长率（rGDP）的Granger原因，而国内生产总值增长率（rGDP）也是财政科技支出增长率（rST）的Granger原因。

第二，财政科技支出增长率（rST）与劳动力总量增长率（rL）之间存在单向的Ganger因果关系。财政科技支出增长率（rST）是劳动力总量增长率（rL）的Granger原因，而劳动力总量增长率（rL）不是财政科技支出增长率（rST）的Granger原因。

第三，财政科技支出增长率（rST）与消费者价格增长率（rCPI）之间存在单向的Ganger因果关系。财政科技支出增长率（rST）是消费者价格增长率（rCPI）的Granger原因，而消费者价格增长率（rCPI）不是财政科技支出增长率（rST）的Granger原因。

第四，财政科技支出增长率（rST）与净出口（NX）之间存在单向的Ganger因果关系。财政科技支出增长率（rST）是净出口（NX）的Granger原因，而净出口（NX）不是财政科技支出增长率（rST）的Granger原因。

然而，Granger因果关系只反映了随机变量之间的统计可预测性，并不能识别经济变量之间的（反事实）因果关系。因此，本书将建立SVAR模型，运用SVAR-IV方法研究财政科技支出政策（rST）的动态因果效应。

构建基准VAR模型。

VAR模型是基于数据的统计意义、将模型中全部变量内生化，用变量的滞后项进行线性表示。基于上面的数据平稳性检验和Granger非因果关系检验，可以用国内生产总值增长率（rGDP）、劳动力增长率（rL）、消费者价格增长率（rGPI）、净出口（NX）以及财政科技支出增长率（rST）数据建立5个变量滞后p阶的基准VAR模型VAR（p）

其中，Yt Yt是5维内生变量列向量，Yt=（rSTt，rGDPt，rLt，rCPIt，NXt）＇Yt=（rSTt，rGDPt，rLt，rCPIt，rBTt）＇，p是滞后阶数，φ1，...，φpΦ1，…，Φp是待估参数矩阵。扰动项ut满足是一个5×5错误！请输入数字。阶的对称正定矩阵。

接下来，对上述构建的基准VAR模型进行稳定性检验，检验的结果如下表5.9所示：

表5.9　VAR模型的单位根检验

从表5.9的稳定性检验结果可知该VAR模型的所有特征根均落在单位圆之外，因此基准VAR模型是稳定的。

由于各个时间序列变量之间可能存在一定的滞后影响，不能同时发生变动，因此在对VAR模型进行估计之前，需要确定最优滞后阶数。本书用Eviews10.0统计软件对VAR模型的最优滞后阶数进行检验，通过似然比统计量（LR）准则、最终预期误差（FPE）准则、赤池准则（AIC）、施瓦茨准则（SC）和HQ准则这五种信息准则检验的结果来进行综合判断，检验结果如表5.10所示：

表5.10　滞后阶数检验结果

从表5.10可以看出，LR信息准则显示最佳滞后阶数为2阶，FPE信息准则显示最佳滞后阶数为5阶，AIC信息准则显示最佳滞后阶数为6阶，SC信息准则也显示最佳滞后阶数为2阶，HQ信息准则显示最佳滞后阶数为5阶，最终依据LR信息准则和SC信息准则的结果确定VAR模型最佳滞后阶数为2阶。

通过上述分析，构建VAR（2）模型

其中，Yt=（rSTt，rGDPt，rLt，rCPIt，NXt）＇Yt=（rSTt，rGDPt，rLt，rCPIt，rBTt）＇，t=1，2，...，T。φj（j=1，2）t=1，2，…，TΦj（j=1，2）是阶自回归参数矩阵；ut ut表示新息冲击向量，各分量分别表示作用在政府财政科技支出增长率、国内生产总值增长率、就业总量增长率、消费者价格增长率以及净出口上的新息冲击，是5×1维白噪声向量。

结构SVAR模型的设定

鉴于VAR模型缺乏经济理论基础，模型新息冲击向量ut ut也没有实际经济含义，为了揭示经济系统对结构冲击的动态响应机制，必须进一步构建SVAR模型以识别真正的政策冲击、研究政策的动态因果效应。

根据变量国内生产总值、就业总量、消费者价格水平、净出口以及财政科技支出之间存在的经济结构关系，本书设定的SVAR模型如下

同样按照VAR模型选择最优滞后阶数的准则，文中选择的滞后阶数为两阶，已知VAR模型的新息向量ut ut与SVAR模型的结构冲击向量εtεt存在ut=Θ0εt关系ut=θ0εt，其中θ0Θ0是5×5 5×5维的非奇异矩阵，且var（εt）=Ik，var（ut）=Σ=，即结构冲击εtεt被假设为相互独立的，并且方差也被正规化为1。因此，基于（5.60）和（5.61）建立的SVAR模型形式如下：

于是，得到滞后算子形式表示

如果矩阵多项式Φ（L）Φ（L）可逆，则SVAR模型（5.63）可以表示为无穷阶SMA（∞）SMA（∞）模型

因此，为得到结果变量对结构冲击的动态因果效应，需要对θ0Θ0进行识别。接下来，本书在前面引入工具变量的SVAR-IV模型理论分析的基础上，选择财政科技支出政策的外部工具变量来识别政策冲击，分析政策对宏观经济的动态因果效应。

实证结果分析

在选择了财政科技支出政策的工具变量后，用工具变量的4期滞后来识别SVAR模型中的政策冲击，得到如下表所示的结果：

表5.11　政策冲击的动态因果效应

表5.11的第一列表示滞后期数，第二列给出了财政科技支出增长率对财政科技支出政策冲击在当期，以及滞后2期、4期、6期、8期、10期、12期、14期、16期时的当期动态因果效应，第三到六列给出了其他四个宏观经济变量对财政科技支出政策冲击在相应各期的累积动态因果效应。

从表5.11第二列的结果可以看到，财政科技支出政策的一个标准差正向冲击造成滞后各期财政科技支出增长率逐渐减弱的正效应，具有较大的拉动作用。从短期来看，财政科技支出政策的一个标准差正向冲击在当期产生的一个标准差正向因果效应正是满足了θ0，11=1Θ0，11=1的标准化单位效应假设，也表明财政科技支出增长率的一个预测方差全部由财政科技支出政策自身的扰动所致；从中长期来看，从滞后2期开始直到滞后16期财政科技支出增长率对财政科技支出政策冲击的动态因果效应依然很强，但逐步减弱，从0.75个标准差的动态因果效应下降到0.13个标准差的动态因果效应，这也验证了我国财政科技支出政策存在一定的惯性。

表5.11第三列反映了财政科技支出政策对国内生产总值增长率具有促进作用，该列数据表示财政科技支出政策的一个标准差正向冲击造成后期国内生产总值增长率的动态因果效应的累积变化，财政科技支出政策的一个标准差正向冲击会对当期和滞后期国内生产总值增长率产生正效应。从短期来看，一个标准差的财政科技支出政策正向冲击在当期会使国内生产总值增长率产生0.38个标准差的正向动态因果效应；从长期来看，到第16期，国内生产总值增长率对政策冲击的累积正向动态因果效应可以达到0.88个标准差。

表5.11第四列反映了财政科技支出政策对劳动力总量增长率会产生抑制的作用，该列数据表示财政科技支出政策的一个标准差正向冲击造成后期劳动力总量增长率的动态因果效应的累积变化，财政科技支出政策的一个标准差正向冲击会对当期及滞后期劳动力总量增长率产生负效应。从短期来看，一个标准差的财政科技支出政策正向冲击在当期就会使劳动力总量增长率产生0.16个标准差的负向动态因果效应；从长期来看，到第16期，劳动力总量增长率对政策冲击的累积负向动态因果效应可以达到0.72个标准差。

表5.11第五列反映了财政科技支出政策对消费者价格增长率具有促进作用，该列数据表示财政科技支出政策的一个标准差正向冲击造成后期消费者价格增长率动态因果效应的累积变化，财政科技支出政策的一个标准差正向冲击会对当期及滞后期消费者价格增长率产生正效应。从短期来看，一个标准差的政策正向冲击在当期使消费者价格增长率产生0.02个标准差的正向动态因果效应；从长期来看，到第16期，消费者价格增长率对政策冲击的累积正向动态因果效应可以达到0.78个标准差。

表5.11最后一列反映了财政科技支出政策对净出口大体上具有促进作用，该列数据表示财政科技支出政策的一个标准差正向冲击造成后期净出口动态因果效应的累积变化。从短期来看，一个标准差的政策正向冲击在当期使净出口产生0.11个标准差的负向动态因果效应；一直到第6期，净出口对政策冲击的累积动态因果效应变为正效应；从长期来看，到第16期，净出口对政策冲击的累积正向动态因果效应可以达到0.07个标准差。

鉴于本书主要考察财政科技支出政策冲击对宏观经济的影响，因此本书主要分析宏观经济对财政科技支出政策冲击的脉冲响应函数。图5.2~图5.5给出了各宏观经济变量对财政科技支出政策冲击的即期脉冲响应图。

图5.2　rGDP对政策冲击的脉冲响应

图5.3　rL对政策冲击的脉冲响应

图5.4　rCPI对政策冲击的脉冲响应

图5.5　NX对政策冲击的脉冲响应

从图5.2中rGDP对政策冲击的即期脉冲响应曲线可以看到，从当期至滞后16期，中国GDP增长率呈现出持续性正向变动情况。给财政科技支出政策的扰动项一个标准差正向结构性冲击后，当期对我国国内生产总值增长率变动产生最大的动态因果效应，有0.38个标准差，随后快速减弱，到滞后8期之后减弱速度有所放缓，并逐步趋向于零，到滞后16期仅有0.01个标准差的正向因果效应。

从图5.3中rL对政策冲击的即期脉冲响应曲线可以看到，从当期至滞后16期，中国劳动力总量增长率呈现出持续性负向变动情况。给财政科技支出政策的扰动项一个标准差正向结构性冲击后，当期对我国劳动力总量增长率变动产生最大的负向动态因果效应，有0.17个标准差，随后各期负向因果效应逐渐减弱，并逐步趋向于零，到滞后16期仅有0.04个标准差的负向因果效应。

从图5.4中rCPI对政策冲击的即期脉冲响应曲线可以看到，从当期至滞后16期，中国CPI增长率呈现出持续性正向变动情况。给财政科技支出政策的扰动项一个标准差正向结构性冲击后，当期对我国CPI增长率变动产生0.02个标准差的动态因果效应，直到滞后10期正向动态因果效应达到最大，有0.12个标准差，随后动态因果效应逐渐减弱，到滞后16期仅有0.07个标准差的正向动态因果效应。

从图5.5中NX对政策冲击的即期脉冲响应曲线可以看到，从滞后2期开始，中国净出口呈现出持续性正向变动且逐渐趋于零的状态，这主要是由于政策冲击对宏观经济变量产生影响存在时滞性。到滞后2期，给财政科技支出政策的扰动项一个标准差正向结构性冲击后，对我国净出口产生最大的正向动态因果效应，有0.07个标准差，影响相对较弱，随后各期正向影响均有所减弱，并逐步趋向于零，到滞后16期仅有0.01个标准差的正向动态因果效应。

弱工具检验

工具变量方法的使用通常会出现弱工具的问题，使得模型估计结果不可靠，出现偏差。本文利用同方差的一阶段F统计量和异方差自相关稳健性检验的两种方法检测工具变量的强弱，结果如表5.12所示：

表5.12　弱工具检验结果

注：表中结果为F值。

从表5.12结果可知，两种检测方法F统计量的值均大于10的临界值，拒绝“工具变量为弱工具”的零假设。本书运用SVAR-IV方法得到的估计结果是可靠的。

可逆性检验结果：上述运用SVAR-IV模型得出的财政科技支出政策对宏观经济的动态因果效应需要以可逆性条件成立为前提，即结构参数矩阵Θ（L）可逆，也就是说可逆性条件是运用SVAR-IV模型进行政策效应分析的前提条件，表5.13是运用Granger非因果检验方法对可逆性条件进行检验的结果。

从表5.13可知，表中各个变量检验的p值均大于5%，因此在5%的显著性水平上认为零假设可逆性成立。这也就说明运用SVAR-IV模型得出的财政科技支出政策对宏观经济的动态因果效应是有效的。

表5.13　可逆性检验结果

注：表中结果为P值。

财政科技支出政策的宏观经济效应是学术界和实务界普遍关注的理论与现实问题，具有极其重要的理论研究价值和实践意义。首先，从短期来看，财政科技支出政策对经济增长具有短期动态调整关系。当期财政科技支出政策对当期经济增长动态因果效应显著，前者每增长1%就会使后者增长0.38%；从长期来看，财政科技支出政策与经济增长之间存在着一种稳定的长期动态均衡关系，财政科技支出政策能够促进经济增长，对经济增长具有明显的拉动作用。其次，从短期来看，财政科技支出政策对劳动力就业具有抑制作用。前者每增长1%就会使后者在当期减少0.16%；从中长期来看，滞后2期到滞后16期财政科技支出政策对就业的挤压作用逐渐减弱。财政科技支出政策对就业的抑制作用正是说明了财政科技支出政策带来的技术进步会减少劳动力市场工作匹配的持续时间，通过直接排斥就业与间接减少工作岗位的双重作用来挤压市场对劳动力的需求，给就业带来了双重“创造性破坏”的负面影响，但是财政科技支出政策冲击对就业产生的负面效应会随着时间的延长而有所减弱。再次，财政科技支出政策冲击对消费者价格增长率产生正向的动态因果效应，从当期到滞后10期，前者每增长1%对后者的动态因果效应逐渐增加，从0.02%的正效应逐渐增加到0.12%的正效应；在滞后10期后，后者的动态因果效应逐渐减小，从0.12%减小到0.07%的正效应。以上表明财政科技支出政策对CPI增长率的正向动态因果效应持续时间较长，但是影响效应相对较弱，财政科技支出政策不能够有效地抑制物价上涨。最后，财政科技支出政策能够有效地刺激净出口、促进国际贸易发展。由于时滞性的影响，政策冲击对净出口的动态因果效应开始于滞后2期，财政科技支出每增长1%就会对净出口产生0.07%的正向动态因果效应，随后正向影响逐渐减弱，一直到滞后16期仅有0.01%的动态因果效应。财政科技支出政策冲击对净出口产生正向动态因果效应说明在一定时期内增加科技领域的财政资金投入，带动的技术进步能够提升产品质量、形成价格优势、降低成本、增强产业竞争力、提升在全球价值链的位置、刺激国际贸易发展。尽管财政科技支出政策对贸易增长具有促进作用，但是这种影响相对较弱。

综上，财政科技支出政策能够促进经济增长、拉动净出口增长，有利于解决我国目前在这两个方面存在的矛盾，有利于我国经济向总量、结构双重平衡靠拢，对国民经济健康、稳定发展产生正面影响。但是，我国当前的财政科技支出政策无法有效地刺激社会就业、抑制通货膨胀。财政科技支出政策对就业的挤压作用以及对物价上升的微弱刺激作用又会对我国经济社会的健康发展产生消极影响。因此，应该合理调整财政科技支出政策，发挥其宏观调控的积极作用，促进我国经济的可持续健康发展。

【注释】

[1]通常GDP增长率序列是随机趋势过程。

[2]例如，我国金融机构一年期人民币存贷款基准利率。

[3]通常GDP增长率序列是随机趋势过程。

[4]自2002年2月以来，金融机构一年期人民币存贷款基准利率分别取值于区间[1.98%，4.14%]和[5.31%，7.47%]；并且，2010年10月20日之前，中国人民银行对一年期存贷款基准利率的调控幅度多为0.27个百分点或0.18个百分点；之后，调控幅度以0.25个百分点为主，或者，较罕见的0.18个百分点。