为了借助误差修正模型的三类系数在政策处理t0前后的变化推断政策处理对结果变量的长短期处理效应,本书利用Chow检验(Chow,1960)和Wald检验(Wald,1943)对政策处理前后误差修正模型的对应系数进行显著差异性的检验。
(1)模型结构检验——Chow检验
假设政策处理前后时间序列的样本观测期分别为t0和t1,即T=t0+t1,分别对前后子样本利用EG两步法估计误差修正模型(4.13)和(4.14)为对应的检验模型形式,并根据全样本T分别估计协整回归模型和误差修正模型
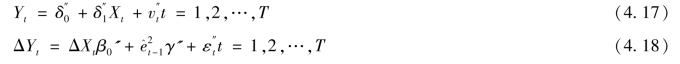
并且,基于协整回归模型(4.5)、(4.6)和(4.17)的系数估计值构造Chow统计量
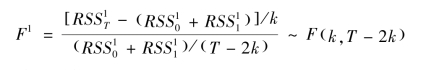
检验零假设
![]()
备择假设
![]()
其中,![]() 分别表示全样本、处理前样本t0和处理后样本t1所对应协整回归模型的残差平方和,k表示待估参数的个数。
分别表示全样本、处理前样本t0和处理后样本t1所对应协整回归模型的残差平方和,k表示待估参数的个数。
再根据误差修正模型(4.13)、(4.14)和(4.18)的系数估计值构造Chow统计量
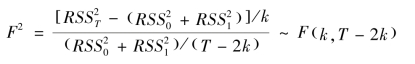
检验零假设
![]()
备择假设
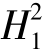 :β0、
:β0、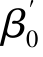 、
、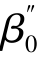 不全相等或γ、γ'、γ″不全相等
不全相等或γ、γ'、γ″不全相等
其中,![]() 分别表示全样本、处理前样本t0和处理后样本t1所对应误差修正模型的残差平方和,k表示待估参数的个数。
分别表示全样本、处理前样本t0和处理后样本t1所对应误差修正模型的残差平方和,k表示待估参数的个数。
于是,若检验统计量Fi ≤Fα(k,T-2k),则接受回归系数无显著性变化的零假设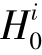 ,即政策处理没有改变模型的结构;若检验统计量Fi>Fα(k,T-2k),则拒绝回归系数无显著性变化的零假设,即政策处理改变了模型的结构(i=1,2)。
,即政策处理没有改变模型的结构;若检验统计量Fi>Fα(k,T-2k),则拒绝回归系数无显著性变化的零假设,即政策处理改变了模型的结构(i=1,2)。
(2)干预前后对应回归系数显著性检验——Wald检验
类似地,也可以使用Wald统计量检验政策处理对结果变量与协变量间长期均衡机制是否平行以及短期修正系数的显著差异性。
首先给出Wald检验的具体步骤:
令f(ω)表示由约束条件组成的列向量,ω^表示无约束估计量,则零假设可以表示为f(ω)=0,定义多个约束条件下的W统计量如下:
![]()
其中,m表示无约束方程中参数的个数;![]() 估计的方差协方差矩阵,计算公式为,
估计的方差协方差矩阵,计算公式为,
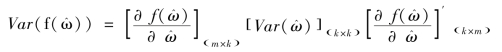
其中,![]() 表示f(ω)用无约束估计量
表示f(ω)用无约束估计量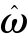 代替后的偏导数矩阵;
代替后的偏导数矩阵;![]() 的估计的方差协方差矩阵;k表示被检验的约束条件的个数。
的估计的方差协方差矩阵;k表示被检验的约束条件的个数。
在约束条件成立的条件下,
![]()
若样本统计量![]() ,则接受原假设,认为约束条件成立。
,则接受原假设,认为约束条件成立。
若样本统计量![]() ,则拒绝原假设,认为约束条件不成立。
,则拒绝原假设,认为约束条件不成立。
以下为政策干预前后模型均衡机制、短期修正系数以及修正速度和短期调整系数的显著性检验:
检验4.1:均衡机制的显著性检验
首先将结果变量与协变量的长期协整回归模型(4.5)和(4.6)设定为
![]()
上式为无约束模型,再利用Wald统计量检验零假设
![]()
即处理前后,变量之间的长期协整关系并未发生显著变化。(https://www.daowen.com)
备择假设
![]()
根据检验结果即可推断政策处理前后的长期均衡机制是否保持不变。若样本统计量![]() ,则接受原假设,认为约束条件成立,即处理前后变量之间的长期协整关系没有发生显著的变化;若样本统计量
,则接受原假设,认为约束条件成立,即处理前后变量之间的长期协整关系没有发生显著的变化;若样本统计量![]() ,则拒绝原假设,认为约束条件不成立,即处理前后变量之间的长期协整关系发生了显著的变化,均衡机制改变。
,则拒绝原假设,认为约束条件不成立,即处理前后变量之间的长期协整关系发生了显著的变化,均衡机制改变。
检验4.2:短期修正系数的显著性检验
为了检验政策处理前后结果变量与协变量间的短期修正系数是否存在显著差异性,将无约束模型设定为
![]()
其中,![]() ,均通过最小二乘估计得到相应的参数估计值。
,均通过最小二乘估计得到相应的参数估计值。
并且,使用Wald统计量检验零假设
![]()
备择假设
![]()
根据检验结果判断政策处理对结果变量与协变量短期修正系数的影响。若样本统计量![]() ,则接受原假设,认为约束条件成立,即处理前后变量之间的短期修正系数没有发生显著的变化;若样本统计量
,则接受原假设,认为约束条件成立,即处理前后变量之间的短期修正系数没有发生显著的变化;若样本统计量![]() ,则拒绝原假设,认为约束条件不成立,即处理前后变量之间的短期修正系数发生了显著的变化。
,则拒绝原假设,认为约束条件不成立,即处理前后变量之间的短期修正系数发生了显著的变化。
检验4.3:修正速度的显著性检验
在检验2的基础上,也可单独检验政策处理前后的修正强度(速度)是否发生显著性变化,即依据无约束模型(4.20),构造Wald统计量检验零假设
![]()
备择假设
![]()
若样本统计量![]() ,则接受原假设,认为约束条件成立,即处理前后修正速度没有发生显著的变化;若样本统计量
,则接受原假设,认为约束条件成立,即处理前后修正速度没有发生显著的变化;若样本统计量![]() ,则拒绝原假设,认为约束条件不成立,即处理前后修正速度发生了显著的变化。
,则拒绝原假设,认为约束条件不成立,即处理前后修正速度发生了显著的变化。
同理,也可以对政策处理前后的短期调整系数β0和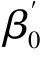 的显著性差异进行检验。
的显著性差异进行检验。
(3)模拟分析
鉴于结果变量和协变量的非平稳性,必须说明使用Chow检验和Wald检验的合理性[2],为此,本书分别对长期关系的Chow检验和Wald检验进行了模拟分析。同时,考虑到样本量(时期数)T和政策处理前时期数T0对实验结果的影响,设定样本量分别为30、100和200,T0/T=0.3,0.5,0.8。
模拟试验的数据生成过程如下:设协变量Xt服从随机游走过程
![]()
处理变量Dt,在T0期之后取值为1,否则取0,即
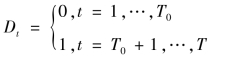
另外,假定模型的误差项εt,νt~i.i.d.N(0,1),为简化数据生成过程,在Chow检验原假设下可设定式(4.5)、(4.6)、(4.17)的参数![]() =1;在Wald检验的原假设下可设定式(4.19)的参数
=1;在Wald检验的原假设下可设定式(4.19)的参数![]() 。
。
对于重复1000次的模拟实验的F值和Wald值,使用单样本的Kolmogorov-Smirnov检验(KS检验)分别推断F值和Wald值是否为F分布和χ2()1分布的随机样本。KS检验是基于累计分布函数的,用于检验一个分布是否符合某种理论分布或比较两个经验分布是否有显著差异[3]。结果见表4.1。
表4.1 检验统计量分布模拟结果和KS检验结果
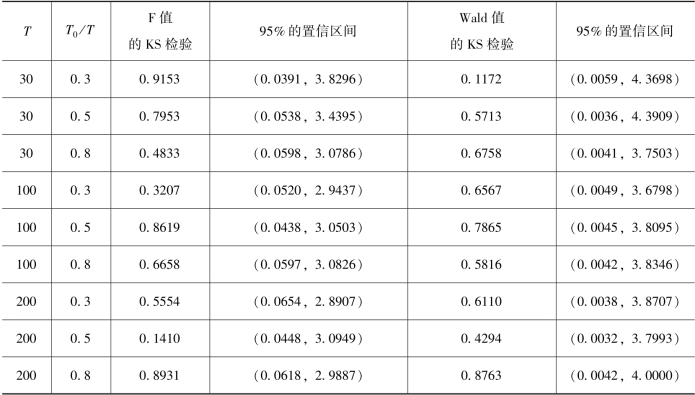
注:KS检验给出的是P值。
从表4.1可知,对于各种设定,F分布和χ2(1)分布的KS检验均不能拒绝原假设,即检验统计量的分布分别服从F分布和χ2分布。另外,由重复模拟的Chow值和Wald值得到相应的概率密度分布图如图4.1和图4.2所示。
在图4.1中实线表示模拟的F检验统计量的概率密度图,虚线表示对应自由度下的标准F分布的概率密度图。由此可见,模拟的Chow统计量分布的概率密度曲线与对应标准分布近乎一致。
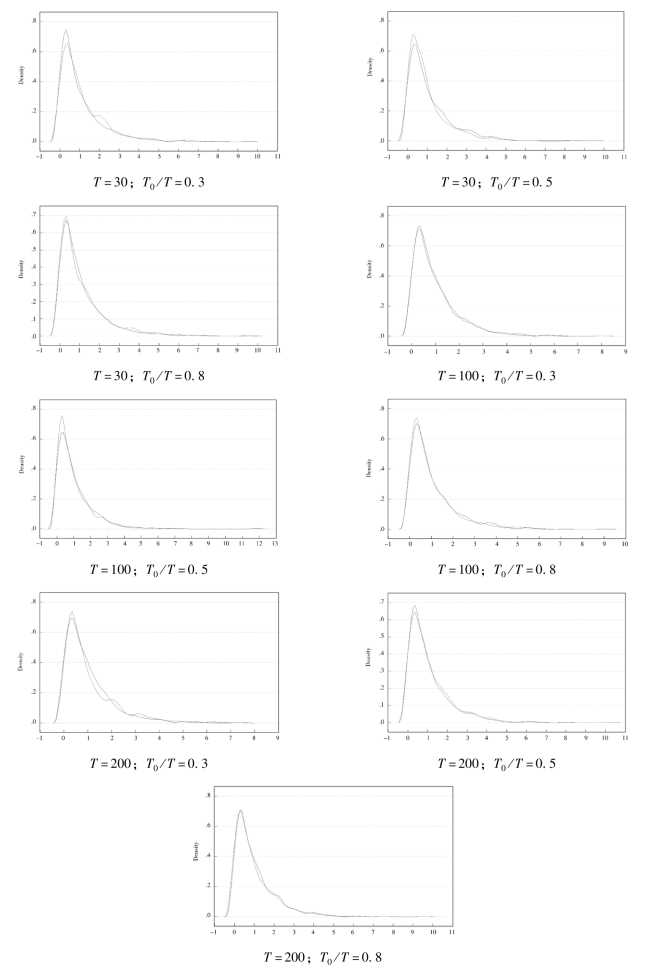
图4.1 F检验统计量的模拟概率密度分布图

图4.2 卡方检验统计量的模拟概率密度分布图
在图4.2中实线表示模拟的Wald检验统计量的概率密度图,虚线表示对应自由度下的标准χ2分布密度图。由此可见,模拟的Wald统计量分布的概率密度曲线与对应标准分布近乎一致。因此,本书对结果变量和协变量非平稳的设定,并不影响Chow检验和Wald检验的合理使用。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







