当然，处理组的结果也可以与一个或多个控制组的结果进行比较，即多组ITS分析。其实验设计包括了一个控制组时间序列和一个处理组的时间序列，并基于时间序列模型：

评估政策干预效应，即检验水平处理效应β6或者趋势处理效应β7是否显著为零；其中，β0到β3表示控制组的参数；β4到β7表示处理组的参数；β4表示处理组和控制组干预前水平值的变化；β5表示处理组和控制组干预前斜率的变化；β6表示处理组和控制组接受干预后水平值的变化；β7表示处理组和控制组接受干预后斜率的变化。变量Z和Dt分别是表示组和处理的二元虚拟变量，

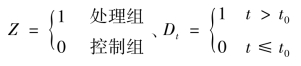
其中，t0是接受处理时间。(www.daowen.com)

例如，Linden&Mi（2015）和Linden&Adams（2011）分别应用多组ITS和倾向得分的多组ITS分析方法研究了美国加州第99号控烟法案的因果效应，并得到了与合成控制法（Abadie et al.，2010）相一致的结论。图3.2给出了多组中断时间序列分析的图示，可见多组中断时间序列分析方法的关键假设是如果处理个体未受干预，两组的结果变量同时发生截距或斜率变化。

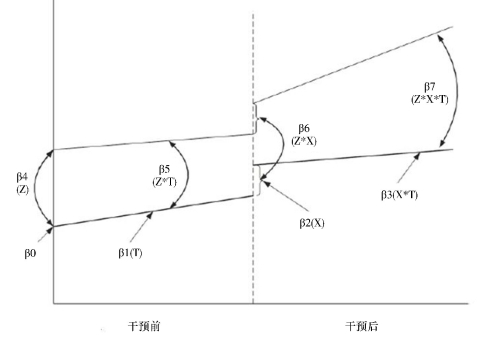
图3.2　多组中断时间序列分析图示

事实上，多组ITS分析的核心是分别析取出两组时间序列的线性时间趋势项，通过推断政策干预前后线性时间趋势项、漂移项和趋势项系数的差异性识别政策因果效应。当存在影响所有个体的外生政策冲击时，多组ITS比单组ITS分析结果更可靠。显然，该方法隐含着两方面的假设，一方面假设时间序列是（二阶矩）平稳的，另一方面因允许两个时间序列存在同期干预效应，只能推断政策干预效应的存在性，不能估计政策干预的平均因果效应；同时只能推断政策干预对（非线性）趋势平稳过程的长期趋势效应，不能区分政策效应的暂时性和持续性。