单组ITS分析仅仅设计了一个接受处理的时间序列，利用时间序列模型

推断水平处理效应β2或者趋势处理效应β3是否显著为零。其中，Dt表示是否接受处理的虚拟变量（处理前取0，处理后取1）；β0表示干预前的截距项；β1表示干预前的斜率；β2表示引入干预后截距项的变化；β3表示引入干预后斜率的变化。图3.1给出了单组时间序列分析的图示。

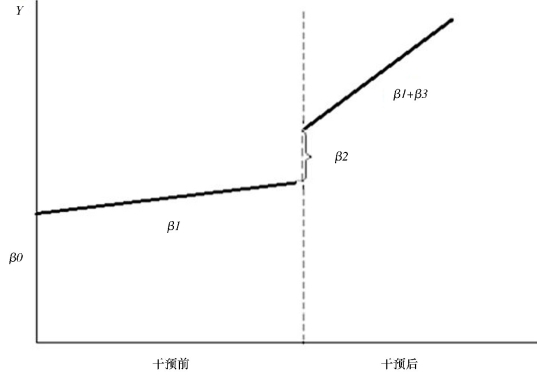
图3.1　单组中断时间序列分析图示

当随机误差项服从一阶自回归AR（1）过程时，即

其中，ρ是指的是相邻误差项之间的相关系数，干扰项μt独立同分布于N（0，σ2）。(www.daowen.com)

ITS方法通过将模型的预测值和反事实结果进行对比，来衡量政策的实施效果。例如，若某样本数据的时间长度为t1，政策干预的时间点为t0，利用模型（3.1）计算第t1时间点的政策效果：

反事实结果为：

则估计的政策因果效应为：

单组和多组模型的识别均由ITS模型的函数形式驱动。按照实验设计，单组ITS没有可比的对照组，将政策干预前的趋势投射到政策实施期间，作为它的反事实。单组ITS假设任何时变的不可测混杂因素都是相对缓慢变化的，这样就能与处理指标（政策实施）的急剧变化区别开来。因此，在单组ITS中，如果政策干预前的趋势平稳，在施加政策干预后结果变量立即发生显著变化并持续一段时间，那么进行因果推断所必需的假设似乎是可信的。需要强调的是，如果在政策干预实施前后的时间窗口中有多个政策变化，抑或在政策干预之前的时间序列中已经存在一种趋势，则需要谨慎使用这一方法。

在Imbens&Lemieux（2008）对中断时间序列分析的稳健性研究中，研究者使用干预前时期的中位数时间点来检验是否存在中断。在一个足够长的时间序列中，选择干预前阶段的中位数时间点作为处理的伪时间点，最大限度地提高检测显著性跳跃的能力。对于较短的时间序列，可以使用每个干预前的时间点作为处理的起始时间点，通过一个简单的迭代过程进行检验。在使用这种稳健性检验时，如果在干预真正开始之前的其他时间点发现结果变量的水平或趋势出现中断，那么单组ITS的基本假设可能会受到挑战，需要设置对照组来排除干预前其他中断因素的干扰。