Hsiao et al.（2012）提出了一种面板数据政策评估方法。与Abadie et al.（2010）的合成控制方法类似，也是利用未受到政策干预的控制组个体的信息来估计处理组个体的反事实结果。为了叙述方便，Hsiao et al.（2012）提出的面板数据政策评估方法简称为“回归合成方法”。回归合成方法的基本思想是：利用截面个体之间的相关性估计处理组个体事后的反事实结果，这种相关性归因于驱动截面个体的共同因子。

假设有N+1个地区共T个时期的面板数据，Y1，it表示个体i在t期受到政策干预时的潜在结果，Y0，it表示个体i在t期没有受到政策干预时的潜在结果，从而个体因果效应为：

Dit表示个体i在t期的处理状态：若个体i在t期受到政策干预，则Di=1；其他取0。个体i在t期的观测结果为：Yit=Dit Y1，it+（1-Dit）Y0，it=Y0，it+τit Dit。假设所有个体的潜在结果服从下列共同因子模型：

其中，αi为个体固定效应，ft为K×1维未观测时变共同因子，bi为因子载荷，εit为误差项，满足E（εit）=0。

可见，ft是所有Y0，it的共同原因，因此所有Y0，it之间是相关的。假定所有Y0，it存在如下预测关系：

利用事前数据（t=1，…，T0，Y1t=Y0，1t）估计模型（2.19），得到。假定如果没有政策干预，所有个体依然保持模型（2.19）的关系。因此，可以利用如下预测模型得到处理组个体事后（t=T0+1，…，T）的反事实结果估计：

因而，相应的政策效应为(www.daowen.com)

由此可见，回归合成方法直接利用控制组观测结果作为处理组个体潜在结果的预测变量。

当事前时期远远大于控制组个体数时，即T0≫N，T0/N→∞，可以利用所有控制组个体作为潜在的合成控制。但是在应用中T0往往是有限的，进入模型的控制组个体越多，回归合成模型的自由度损失越多，估计精度会降低。因而，在模型拟合时存在着拟合程度与估计精度之间的权衡。Hsiao et al.（2012）提出了一种两步法用于控制组的选择。

（1）分别引入1个控制组个体作为协变量进行回归，共需要进行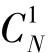个回归，然后从中取R2或似然值最大的模型作为M（1）；

同理，引入2个控制组个体，进行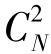个回归，选出M（2）；

以此类推，直到得到模型M（N）。

（2）从M（1），…，M（N）中选择AIC或AICC最小的模型M（m），M（m）对应的权重就是最优的合成控制组权重。