（1）线性回归法

广泛应用于经济学经验研究的回归分析方法是一种标准的统计推断方法，普通的回归模型只揭示了解释变量与被解释变量之间的统计相关性，不能反映因果关系。但是，Mill（1974）率先提出了利用回归模型进行因果推断的差异法（Method of Difference），即当变量X成立时Y的结果与X不成立时Y的反事实结果的差异在统计上是显著的，则称变量X对Y是有因果影响的。之后，Holland（1986）指出在其他条件不变时，比较某一现象出现和不出现对结果变量的差异就是这个原因产生的因果效应。因果效应参数被定义为条件期望函数（Conditional Expectation Function，CEF），显然，如果CEF揭示了因果效应，那么回归模型就可用于因果推断。

特别地，对于含有二元处理变量Di和可观测控制变量Xi的线性回归模型

假设2.1 条件独立性假设（Conditional Independence Assumption，CIA）

以及

假设2.2 共同支撑假设（Overlap）

时，则处理变量Dt的回归系数

其中，τX=为条件期望之差。即回归系数τD是对条件期望之差τX的加权平均，线性回归模型的系数揭示了处理变量对结果变量的因果效应。

显然，利用线性回归法识别因果效应的关键在于对混杂因素Xi的控制，根据赵西亮（2017）和Angrist&Pischke（2009）的描述，好的控制变量（Good Control）一般是发生在原因变量之前的或者不受原因变量影响的变量，即良好的控制变量是隐含的混杂因素。另外，模型的误设也会导致对处理效应的估计偏误。例如Cochran&Rubin（1973）和Rubin（2001）等均发现协变量与结果变量之间非线性关系也会导致对处理效应估计的偏差。为此，Hahn（1998）提出了因果效应的非参数估计方法，Heckman et al.（1998）则利用核估计方法估计因果效应。Angrist&Piscke（2009）、洪永淼（2011）和Morgan&Winship（2015）等文献讨论了回归模型以及因果效应参数之间的关系。

（2）匹配方法和逆概率加权法

①匹配方法

为了解决处理组个体反事实结果的估计问题，Gu&Rosenbaum（1993）、Heckman et al.（1998）、Dehejia&Wahba（1999）和Abadie&Imbens（2016）等文献提出并研究了因果效应的匹配估计方法。匹配估计方法的基本原理是在条件独立性假设下，对于每个处理组个体从控制组中匹配一个与其具有相似特征的个体——匹配样本，并利用匹配样本的观测结果估计处理组个体的反事实结果。样本匹配方法通常分为协变量匹配法和倾向得分匹配（Propensity Score Matching，PSM）方法，他们依赖于协变量Xi的维度，倾向得分匹配法通常适用于高维协变量等的情形。事实上，倾向得分匹配方法的核心源于Rosenbaum&Rubin（1983）证明的倾向指数定理，Dehejia&Wahba（1999）等用在了横截面数据的因果推断中。倾向指数定理如下：

如果{Y0i，Y1i}⊥Di|Xi成立，则有{Y0i，Y1i}⊥Di|p（Xi）。(www.daowen.com)

于是，在假设2.1和假设2.2的条件下，根据倾向得分p（Xi）匹配的控制组个体的观测结果可以估计处理组个体的反事实结果。并且，估计倾向得分常用Probit模型、Logit模型，或者Heckman et al.（1998）和Ichimura&Linton（2003）提出的非参数核估计模型。另外，Abadie&Imbens（2006，2016）分别研究了协变量精确匹配和倾向得分匹配方法估计因果效应的问题。

另外，在倾向得分估计的基础上，Robins et al.（1992）利用逆概率（倾向得分的逆）对样本进行加权调整后估计因果效应，即因果效应的逆概率加权（Inverse Probability of Treatment Weighting，IPW）估计方法；Robins&Rotnitzky（1995）提出了双稳健估计方法。特别，匹配估计方法的应用研究文献较为丰富，例如，Dehejia&Wahba（1999）研究了培训项目对个人收入的影响，Gilligan&Hoddinott（2007）用PSM评估了埃塞俄比亚2002年应急食物救援政策的因果效应，陈飞和翟伟娟（2015）研究了农户土地流转决策的福利效应。

匹配法的缺点是只能基于可观测变量进行匹配，不能控制不可观测因素导致的异质性；此外，匹配所得的样本的协变量分布可能与总体的分布不一致，基于匹配样本所估计的因果效应不能推广到整个总体，仅为较小的子总体提供一个现实的估计。且匹配法实施的前提是非混杂性假设，针对该假设的敏感性分析，Heckman（2008）认为当存在不可观测的混杂因素时，倾向得分匹配非但不能消除选择性偏差，反而会带来新的偏差；刘凤芹和马慧（2009）也发现倾向得分匹配方法对非混杂性假设是非常敏感的；Damrongplasit et al.（2010）对比了参数方法和倾向得分匹配方法的结果，进一步验证了倾向得分匹配的实施需要满足非混杂性假定。

具体实施匹配时，除了个体之间的匹配，还可以分层匹配（stratification），对样本进行分层以调整选择偏差（Rosenbaum&Rubin，1983）。根据协变量或者倾向得分分层后，每一层内均类似于完全随机化实验，因此，层内因果效应是可以识别的。通常的做法是根据倾向得分分层，先估计倾向得分的值，然后将样本划分成具有相似倾向得分的层（通常基于倾向得分的分位数进行划分），相同层内的个体具有相似的协变量分布。在每一层内估计各子总体的处理效应，而总体的平均处理效应则由各层的平均处理效应加权得出。其中层的数量取决于数据集的大小，Rosenbaum&Rubin（1984）的研究表明，划分为5个层可以消除超过90%的估计偏差。Hullsiek&Louis（2002）指出，层数的增加可以进一步地减少估计偏差，但可能以方差的增加为代价。

②逆概率加权法

倾向得分作为一种降维工具，除了用于匹配以平衡组间的协变量分布之外，还可以用于样本的加权调整，常用的加权调整法是逆概率加权。IPW是一种类似于标准化的统计技术，起源于60多年前的调查研究，后被Robin et al.（1992）引入观察性研究的因果推断中。

首先构造逆概率（倾向得分的倒数）权重，然后利用该权重对观测样本加权，从而构造一个虚拟总体，在该虚拟总体中，协变量分布与分配机制相互独立，达到近似于随机实验的目的，可消除由协变量不平衡引起的估计偏差（Rosenbaum，1987）。在非混杂性假设下，可以证明：

在实际应用中，首先拟合一个处理概率参数模型：

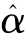倾向得分满足矩方程E[Z-π（Z；α）]=0，可用GMM来估计未知参数α，得到之后，平均因果效应的逆概率加权估计为：

该方法隐含的假设是处理概率模型是正确的，如果是，那么加权后的样本可视为来自随机实验（Hernán&Robins，2016）。但是在实践中，处理概率模型是否包含了所有关键协变量是不可知的，协变量的选择影响倾向得分进而影响到逆概率加权估计量的稳定性。鉴于此，Robins et al.（2000）和Hirano et al.（2003）分别构造了倾向得分逆概率的替代估计量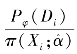[Pφ（Di）是D的边际分布]和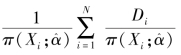用以减轻不稳定性。

上述回归方法是基于回归调整的估计策略，匹配和逆概率加权方法是基于处理分配概率的估计策略，所得因果效应是否有偏依赖于回归模型和处理概率模型是否正确设定。近年来，将这两种类型的估计策略结合使用以防止由于模型错误设定而产生偏差的方法变得越来越流行。双重建模方法拥有“双稳健性”（double robust），这意味着如果正确设定了这两类模型中的任何一个，估计量将具有一致性（Van der Laan et al.，2003）。