在经典的随机实验中，个体处理状态是随机分配的，分配不依赖于个体的潜在结果，并且分配概率是已知的。根据分配机制的设定不同，可以分成四类：

（1）Bernoulli实验

在Bernoulli实验中，可以利用投硬币方式决定每个个体的处理状态。硬币可以是不均匀的，即每个个体进入处理组的概率为p。在Bernoulli随机实验中，可能会出现所有个体均在处理组或控制组的情况。当所有个体均在处理组或控制组时，就没有办法通过两组个体结果的比较进行因果推断。这是Bernoulli实验的一个主要缺点。

（2）完全随机实验

假定共有N个个体，随机地选择其中的Nt个个体进入处理组，其余Nc=N-Nt个个体进入控制组。这种方式的随机实验称为完全随机实验。完全随机实验的分配机制满足如下两个条件：

独立性假设：处理状态Di是随机分配的，即{Y0i，Y1i}⊥Di

共同支撑假设：既有处理组个体，又有控制组个体，即0＜P（Di=1）＜1

在完全随机实验中，处理状态的随机分配意味着，{Y0i，Y1i}⊥Di，即处理变量Di的取值独立于两个潜在结果{Y0i，Y1i}。这意味着如下两式成立（均值独立）：

因而，随机实验可以消除选择性偏误。此时，两组观测结果的均值之差就是ATE。

在线性回归分析中，通常需要施加零均值或模型正确设定的假设，要求以解释变量为条件，误差项的条件期望值为零，即

在实际应用中，这一假设无法检验，也无法保证，但是在随机化实验中却可以得到保证。假定观测结果Yi可以利用潜在结果和处理变量表示，即

以上推导利用了随机化实验中干预分配独立于潜在结果的结论。因此，在完全随机化实验中，回归方程（2.3）满足随机误差条件期望为零的假设。由此，对于完全随机化实验数据，且假定所有个体的因果效应都相同，一元回归模型没有内生性，则可以利用线性回归进行分析，构造模型如下：

此时，我们赋予了回归系数τ因果含义。可见，一元线性回归的最小二乘估计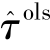就是平均因果效应参数τATE的无偏估计。

（1）分层随机实验

假设在随机实验中，某些个体特征或变量X对潜在结果有重要影响，这时，可以首先根据变量X进行分层（stratification），然后在层内再实施完全随机实验，这种实验称为分层随机实验。用Xi表示作为分层依据的协变量，那么，分层随机实验的分配机制满足如下两个条件：

式（2.5）称非混杂性或条件独立性，即以协变量Xi为条件，潜在结果独立于干预分配，或者说，根据协变量Xi分层，层内是完全随机化实验，从而相同Xi的群体中，潜在结果是独立于处理变量的。此时，有条件均值独立性（CMI）成立：(www.daowen.com)

式（1.6）表示，在Xi分层内，处理组的反事实结果可以用控制组的观测结果来估计；式（1.7）反之。此时，处理组的平均因果效应可以表示为：

若Xi是离散的，ATT可以表示为：

同理，ATE可以表示为：

其中，τX=E（Yi|Xi，Di=1）-E（Yi|Xi，Di=0）为层内观测结果的差异。

由以上分析可知，如果数据不是来自完全随机实验，则E[ui|Di]不一定为零。

即可能存在内生性，此时一元回归的OLS估计是有偏的。但如果数据来自分层随机实验，满足条件独立性假设，则Di与ui相关的唯一原因是Di与ui中可观测变量Xi相关。将ui分解为：

则一元回归方程（2.4）可写作

此时，有E（εi|Xi，Di）=E（εi|Xi）成立。如果数据来自分层随机实验，且假定所有个体的因果效应都相同，则多元回归中τ的OLS估计就是ATE的无偏估计量。

（2）配对随机实验

配对随机化实验是一种特殊的分层随机化实验，每层只有两个个体，这两个个体在层内随机化分配，一个进入处理组，一个进入控制组。因而，每层内的平均因果效应可以用处理个体和控制个体观测结果之差进行测度，即

总体的平均因果效应可以表示为：

可以建立回归方程进行分析：

如果引入协变量，可以采用下列回归方程：

方程（2.9）和（2.10）的常数项即为总体平均因果效应的估计。

综之，随机化实验的作用是平衡处理组和控制组个体其他因素的分布，从而使得两组个体具有可比性。随机实验能够解决潜在结果模型中的缺失数据问题，因此理想的随机化实验是自然实验中识别因果关系并实现因果推断的基准。Rubin（1974）将随机实验中的因果效应识别策略推广到了观察性研究，关键之处是思考如何设计分配机制以向随机化实验靠拢。Rubin因果模型为因果效应的定义和因果推断提供了一种基于实验视角的解决途径，推动了因果研究的复兴，现已成为统计学和计量经济学研究中有关因果推断问题的标准分析框架，并为其他各学科的因果研究提供基础性理论和方法论指导。目前，实验学派已经成为经济学因果研究中的新主流（Angrist&Pischke，2010），Rubin因果模型被广泛应用于经济政策效应的评估研究领域。