本书采用多目标综合决策的层次分析法，建立测度港口区位势的数学模型。层次分析法（AHP）是美国运筹学家萨蒂（Saaty）于20世纪70年代提出的一种多准则决策方法。它是一种新的定性与定量分析相结合的系统分析方法。由于AHP具有完备的数学理论基础、严格的逻辑推理、非结构化向结构化转换的功能、描述问题实用等特点而受到越来越多的重视和运用。AHP实质是一种决策思维方式，其最大的贡献在于对人的主观判断做出了客观的定量描述。AHP解决问题的基本思路：从系统的层次性特征出发由高到低划分成若干层次，建立一个树状层次分析结构以描述元素之间的相互关系。根据对一定客观现实的判断，就每一层次的元素相对于上一层元素的重要性给予定量表示，利用数学方法，确定表达每一层次的全部元素的相对重要次序的权值，通过对结果进行排序，对问题进行分析和决策（王莲芬、许树柏，1990；陈湛匀，1991）。整个过程逻辑结构如图5-2所示。

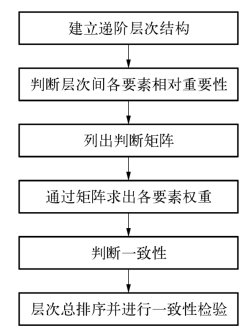
图5-2　层次分析法逻辑结构图

1）港口区位势测度的递阶层次结构

港口区位势测度的递阶层次结构如图5-3所示。

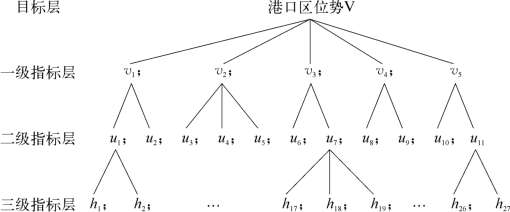
图5-3　港口区位势测度的递阶层次结构

2）构造两两比较判断矩阵

在建立递阶层次结构以后，上下层之间元素的隶属关系就确定了。假定上一层次的元素Ck作为准则，对下一层次的元素A1，A2，…，An有支配关系，其目的是在准则Ck下按照它们的相对重要性赋予A1，A2，…，An相应的权重。AHP是用两两比较的方法来获得相对权重。通过对各个元素进行反复的两两比较，得出每个元素相对于其他元素的相对重要比率，然后将元素的比较结果综合起来，得出元素的综合权重。这里需要对重要程度赋予一定的数值。一般使用1～9来标度，其含义如表5-1所示。

表5-1　重要性标度及其含义

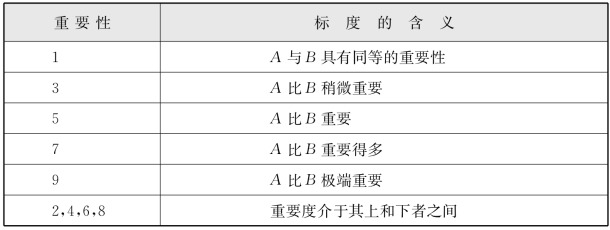
资料来源：施欣.水运企业现代管理理论方法与应用［M］.北京：人民交通出版社，2000.

采用1～9的重要性标度方法是将思维判断数量化的一种较好的方法。首先，在区分事物质的差别时，人们总是用相同、较强、强、很强、极端强的语言。再进一步细分，可以在相邻的两极中插入折中的提法，因此对于大多数决策判断来说1～9级的标度是适用的。其次，心理学实验表明，大多数人对不同事物在相同属性上差别的分辨力在5～9之间，采用1～9的标度能反映多数人的判断能力。最后，当被比较的元素的属性处于不同的数量级时，一般需要将较高数量级元素进一步分解，这可以保证被比较元素在所考虑的属性上有同一个数量级或比较接近，从而适用于1～9的标度。

对于n个元素来说，通过两两比较，可以得到两两比较判断矩阵A：

判断矩阵具有如下性质：

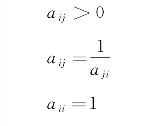
3）计算单一准则下元素的相对权重

这一步要解决在准则Ck下，n个元素A1，A2，…，An排序权重的计算问题，并进行一致性检验。对于A1，A2，…，An通过两两比较得到的判断矩阵A，解特征根问题：AW=λmaxW。

所得到的W经正规化后作为元素A1，A2，…，An在准则下的排序权重。这种方法即排序权向量计算的特征根方法。λmax存在且唯一，W可以由正分量组成，W也是唯一的。一般可采用和积法求Wi：(www.daowen.com)

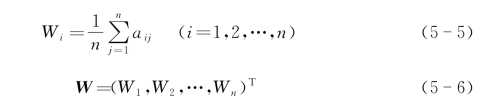
采用近似算法求λmax：

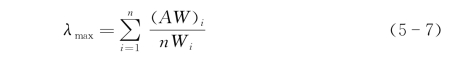
4）判断一致性

为了判断各元素的逐对比较结果是否符合一致性，需要计算一致性指数，再根据一致性辨别公式：CR=CI／RI做出判断。RI可查平均随机一致性表（见表5-2）得到。

表5-2　RI平均随机一致性表

资料来源：施欣.水运企业现代管理理论方法与应用［M］.北京：人民交通出版社，2000.

若CR=CI／RI＜0.1，则符合一致性判断，即认为该判断矩阵具有满意的一致性，就可依次确定各元素的权重。

5）计算港口区位势

式中，Vi为研究对象i港口区位势，由港口区位势评价指标体系中的一级指标vj加权平均后得出。vj（j=1，2，…，5）分别表示i港口自然区位势、港口运输区位势、港口经济区位势、港口技术区位势和港口管理区位势，w为一级指标权重，则有：

式中，uk为评价指标体系的二级指标，经评价指标体系中的第三级指标加权平均后得出，w′为各二级指标的权重，则有：

式中，hl为评价指标体系的三级指标，为各三级指标的权重。

6）港口相对区位势模型

研究的特定区域中，某一港口在区域港口群体集合中获取或供应与港口相关活动区位要素的相对能力即为港口相对区位势。

式中，Pi为i港口在研究对象区域内的相对区位势，是指i港口在该区域港口群体集合中区位发展的相对潜力与吸引力，反映了i港口所占据的地位与发挥的作用，是划分枢纽港、干线港和喂给港的重要依据之一。