空间相互作用区位引力模型主要为求出区域内两个地点之间存在的相互作用量的大小而提出的。最早的引力模型是将牛顿的万有引力定律移植到社会经济问题的研究领域，因而又称为“牛顿模型”（或“重力模型”）。

1687年，牛顿提出著名的万有引力定律：在两个具有质量m1和m2而相距dij的物体间，存在一个相互吸引的万有引力F，其大小与两物体的质量mi和mj成正比，与两物体间的距离dij的平方成反比，数学表达式为：

1929年，美国学者赖利（Reilly）对得克萨斯州225个商业零售区进行了考察，发现商业零售区的规模越大，它从周围吸引到的顾客预期数量就越多。就距离而言，一个商业零售区从附近地区吸引到的顾客预期数量比从较远的地区吸引到的顾客预期数量要多。这与牛顿万有引力定律反映的物理现象之间具有极大的相似性，于是他借鉴物理学的万有引力定律，提出商业区的“零售引力法则”，即商业区对外部某一地点的吸引力与商业区自身规模成正比，与两者之间的距离的平方成反比。商业区自身规模反映的是其市场的供应能力，用营业面积或营业量表示。

在图3-1中，商业区i的规模为Si，商业区j的规模为Sj，它们之间分布着消费者线形市场，其中某一点x处有消费者规模Px，Tix和Tjx分别表示商业区i和商业区j对x点的吸引力。

图3-1　商业区对线形市场的分割

则有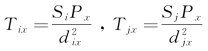，两式相除，即得：(www.daowen.com)

赖利的主要贡献不在于上述十分基本的公式，而是在此基础上发展了一个识别空间中零售商控制市场范围界限的模型，即提出了划分商业区吸引范围的“市场边界辨识法”（market boundary identification technique）。赖利认为，辨识两商业区的市场边界，其实质就是寻找与两商业区吸引力的平衡点，该点被定义为断裂点（breaking point）。求断裂点的步骤如下：

设x点为断裂点，则Tix=Tjx，即有；取d=dix+djx，容易求得：

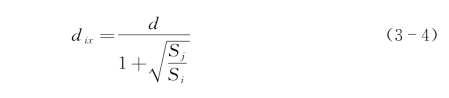
断裂点的实质是由一个吸引中心的市场优势区域转变为另一个中心的市场优势区域的转折点。将求出商业区i和周围若干个相邻的商业区j之间的断裂点，用平滑曲线连接起来，就可得到商业区i的吸引范围。

继赖利之后，引力模型成了地理学、经济学和规划工作的通行模型，并根据社会现象的复杂性对引力模型进行修正，得到地理空间相互作用的通用引力模型，其一般表达式为：

式中，Tij表示两个区位（城市、聚落或经济点等）的交互作用量（人流、业务流、资金流、信息流等），Pi，Pj除了用人口规模来表示外，也可以用商业的零售额、就业机会、工业总产值、固定资产和流动资金等其他替代指标来表示，并根据两地间的年龄结构、消费水平、就业水平或生产率水平等方面的差异，加入不同的指数α，β。距离因素（dij）也可以用多种方法测量，除了最常用的两地之间的地理距离外，还可用时间距离（当考虑路况条件时）、经济距离（考虑不同交通工具的成本时），甚至可用当考虑历史文化等因素时的心理感应距离来测量；b称为距离摩擦指数，b值越大，则表示随着距离的增加，相互作用量的衰减速度越快（杨吾扬、梁进社，1997）。