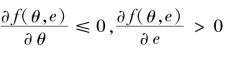本文考虑如下的经济环境：首先，中央政府委托地方政府进行生产，进而实现q单位的经济增长质量，中央政府从q单位的经济增长质量中获得效用S（q），且满足S′＞0，S″＜0。其次，地方政府提升经济增长质量面临着转换成本。其中，转换成本函数（C）被定义为：C（θ，e）=θeq（θ，e）。其中，θ和e分别为边际转换成本和努力水平。再次，由于存在着信息不对称，中央政府无法观察到地方政府提升经济增长质量的转换成本和努力程度，但以下事实是双方的共识，即：，其累计分布函数为F=F（θ，e），概率密度则为f（θ，e）＞0，且满足^[6]；（3）地方增长质量（q）被定义为：q=（θ，e）。最后，地方政府的效用函数（U）被定义为：U=U（θ，e）=t[q（θ，e）]-θeq（θ，e）。其中，t[q（θ，e）]为地方政府提升经济增长质量的晋升收益。

根据图1所示，此博弈的时间线为：在阶段1，地方政府首先获取了提升经济增长质量的边际转换成本（θ）（构成了地方政府的私人信息）；随后在阶段2和3，中央政府提供一组晋升契约，供地方政府选择；在阶段4，地方政府根据中央政府提供的激励契约执行努力水平e，并最终在阶段5实现增长质量，进一步获得相应的晋升收益t（q）。

图1　地方政府提升增长质量的博弈结构

在连续情形下，地方政府提升经济增长质量的参与约束可以被表示为：

假设存在着一个真实的显示机制，那么式（2）成立，即：

根据式（2），可以解得真实显示机制的一阶条件：

为了使真实的显示机制成为最优的机制，对于所有的θ和e，还必须满足：

同时，局部的二阶条件仍然是必要的，即：

对式（4）求微分，还可以得到：

式（6）说明，转换成本与对经济增长质量具有抑制作用，转换成本越高，增长质量越低。同时，式（4）和（6）构成了一个局部的激励相容约束，它确保了地方政府在局部上会真实显示自己的偏好。利用式（3）和（4）还可以证明：

这保证了局部的激励相容约束同时还是全局的激励相同约束。因此，式（4）和（6）便构成了最终的激励相容约束。

进一步，我们使用U=U（θ，e）=t[q（θ，e）]-（θ+e）q（θ，e）代替转移支付，局部的激励相容可以被表示为：

因此，地方政府的激励相容约束便可以被表示为：

那么，中央政府的优化问题便可以被表述为：(www.daowen.com)

首先利用式（11）和（12）求解上述规划问题，构造Hamilton函数：

其中，λ为共状态变量，U为状态变量，q为控制变量。

由最优化控制原理，得：

对式（15）积分，得：

对q（·）求导，则再利用式（16），则最优化条件为：

而在不存在转换成本差异的条件下，最优条件则退化为：

相应的保留效用和转移支付水平为：

通过式（8）、（9）、（19）和（20）可以发现：第一，在不存在边际转换成本差异的条件下，“激励”问题成为地方增长质量提升的核心问题，地方政府努力提升经济增长质量，获得晋升收益。且晋升收益越大，地方政府提升经济增长质量的效用越强，努力水平也越高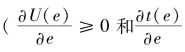≥0），最终实现的经济增长质量也越高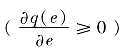，即：t↑→U↑→e↑→q↑。

第二，如果提升经济增长质量的边际转换成本存在着差异，提升经济增长质量将不仅面临着“激励”问题，还同时面临着“信息”问题。随着边际转换成本的增大，地方政府提升经济增长质量的转移支付和效用水平减小^[7]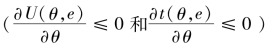，从而导致地方政府提升经济增长质量的努力水平较低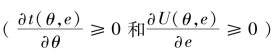，最终导致实现的经济增长质量也较低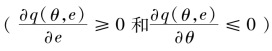，即：θ↑→U↓→t↓→e↓→q↓。

根据式（6）和以上讨论可以发现：转换成本与经济增长质量间存在着负相关系。如果不考虑地方政府提升经济增长质量的转换成本，通过提供晋升收益将提高地方政府提升经济增长质量的努力水平，并最终实现合意的经济增长质量；与之相对应，在转换成本存在着差异的前提下，转换成本的差异性决定了地方政府质量激励的“异质性”。随着边际转换成本的增大，地方政府提升经济增长质量的效用水平和转移支付越低，地方政府改善经济增长质量的意愿也较小，最终导致所实现的地方经济增长质量较低。当边际转换成本较大时，充分有效的激励（晋升激励）也不会提高地方增长质量。

根据以上讨论，本文提出以下可供验证的研究命题：

命题1：地方政府提升增长质量的转换成本越大，地方增长质量也越低。

命题2：当转换成本较小时，晋升激励对地方增长质量的促进作用较高；反之，晋升激励对地方增长质量的促进作用较小。