最简单的存贮模型,即需求不随时间变化的确定型存贮模型。这类模型的有关参数如需求量、提前订货时间是确定的值,而且在相当长一段时间内稳定不变。实际上,只要企业所考虑的参数的波动性不大,就可认为是确定型的存贮问题。经过数学抽象概括的存贮模型虽然不可能与现实完全等同,但对模型的探讨将加深我们对存贮问题的认识,其模型的解也将对存贮系统的决策提供帮助。

1.经济订货批量的概念

经济订货批量(Economic Order Quantity,EOQ)模型又称整批间隔进货模型,该模型适用于整批间隔进货、不允许缺货的存贮问题,即某种物资单位时间的需求量为常数D,存贮量以单位时间消耗数量D的速度逐渐下降,经过时间T后,存贮量下降到零,此时开始订货并随即到货,库存量由零上升为最高库存量Q,然后开始下一个存贮周期,形成多周期存贮模型。

由于需求量和提前订货时间是确定的,因此只要确定每次订货的数量或进货间隔时间,就可以做出存贮策略。由于存贮策略是以存贮总费用最小的经济原则确定订货批量,故称该订货批量为经济订货批量。

2.EOQ模型

(1)模型假设

存贮某种物资,不允许缺货,其存贮参数为:

T:存贮周期或订货周期(年,月,日);

D:单位时间需求量(件/年,件/月,件/日);

Q:每次订货批量(件/个);

C1:存贮单位物资单位时间的存贮费[元/(件·年),元/(件·月),元/(件·日)];

C2:每次订货的订货费(元,万元);

t:提前订货时间为零,即订货后瞬间全部到货。

(2)建立模型

存贮量变化状态如图4-4所示。

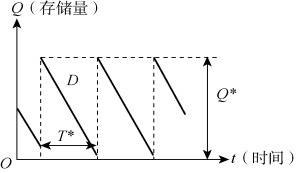
图4-4　存贮量变化状态

一个存贮周期内需要该种物资Q=DT个,图中存贮量斜线上的每一点表示该时刻的库存水平,每一个存贮周期存贮量的变化形成一个直角三角形,一个存贮周期的平均存贮量为1/2Q,存贮费为1/2C1QT,订货一次费用为C2,因此,在这个存贮周期内存贮总费用为1/2C1QT+C2。

由于订货周期T是变量,所以只计算一个周期内的费用是没有意义的,需要计算单位时间的存贮总费用CZ,即

CZ=1/2C1Q+C2/T

将T=Q/D代入上式,得:

CZ=1/2C1Q+C2 D/Q(www.daowen.com)

显然,单位时间的订货费随着订货批量的增大而减小,而单位时间的存贮费随着订货批量Q的增大而增大,如图4-5所示。从图4-5可直观看出,在订货费用线和存贮费用曲线相交处,订货费和存贮费相等,存贮总费用的曲线取得最小值。

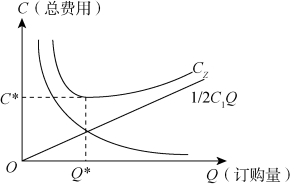
图4-5　存储费用曲线图

利用微分求极值的方法,令d CZ/d Q=1/2C1-C2 D/Q2=0,即得到经济订货批量Q*:

由经济订货批量公式及Q*=T*D,可得到经济订货间隔期:

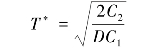
将Q*值代入CZ=1/2C1Q+C2 D/Q式,得到按经济订货批量进货时的最小存贮总费用:

需要说明的是,在确定经济订货批量时,进行了订货和进货同时发生的假设,实际上,订货和到货一般有一段时间间隔,为保证供应的连续性,需提前订货。

设提前订货时间为t,日需要量为D,则订购点s=D·t,当库存下降到s时,即按经济订货批量Q*订货,在提前订货时间内,以每天D的速度消耗库存,当库存下降到零时,恰好收到订货,开始一个新的存贮周期。

另外,以实物计量单位如件、个表示货物数量时,Q*是每次应订购的物资数量,若不是整数,可四舍五入后取整。

对于以上确定型存贮问题,最常使用的策略就是确定经济订货数量Q*,并每隔T*时间订货,使存贮量由s*(往往以零计算)恢复到最高库存量S=Q*+s,这种存贮策略可以认为是定量订购制,但因订购周期固定,又可以认为是定期订购制。

例:某车间需要某种标准件,不允许缺货,按生产计划,年需要量10 000件,每件价格1元,每采购一次的采购费为25元,年保管费率为12.5%,该元件可在市场上立即购得,问:应如何组织进货?

解:经济订货批量: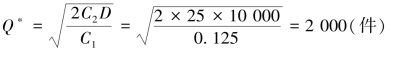

经济订货周期:

如以D表示某种物资的年需用量,V表示该物资的单价,C2为一次订货费,r表示存贮费率,即存贮每元物资一年所需的存贮费用,则得到经济订货批量的另外一种常用形式:

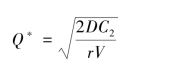
3.EOQ模型的敏感性分析

EOQ模型中所涉及的物资需用量、存贮费、订货费等参数,一般根据统计资料并估计计划期的发展趋势而确定,往往与实际情况有一些误差。另外,经济订货批量往往不是整数,而实际订货时,常常要求以一定的整数如整桶、整吨等单位进行订货,为此,我们需要分析模型的各项参数发生偏差时对经济订货批量Q的影响程度,以及经济订货批量的偏差对存贮总费用的影响程度,从而考察EOQ模型的可靠程度和实用价值,即对EOQ模型进行敏感性分析。

物资存贮中通常会遇到其他一些附加条件,如物资单价按订货批量进行的折扣;所存贮物资占用的流动资金有一定数额限制;仓库库容有一定限制;多种物资同时订购的比例等,这些模型的表现形式更为复杂,但在具体分析时都是本着综合平衡各种费用和成本的原则,使总的存贮费用最低。