1.实验目的

（1）用计算机与电子天平联用。用沉降法测定滑石粉的粒度分度。

（2）了解计算机与电子天平联用测绘沉降曲线、拟合曲线方程、研究粒度分布的原理与方法。

2.实验原理

粒度分布测定是指使一悬浮液中的粒子在重力场作用下而沉降，从不同时间内的沉降量求得不同半径粒子相对量的分布。它的测定理论根据是基于斯托克斯（Stokes）定律的力平衡原理：假设半径为r的球形粒子在重力作用下，在黏度为η的均相介质中以速度为υ做等速运动，则粒子所受到的阻力（摩擦力）f由下式决定：

由于粒子做等速运动，所以这一摩擦力应等于粒子所受的重力 ，即

式中，η为介质黏度（Pa·s）；υ为粒子沉降速度（m·s-1）；ρ为粒子密度（kg·m-3）；ρ0为介质密度（kg·m-3）；g为重力加速度（m·s-2）。

由式（3-98）可得

若已知η、ρ、ρ0，则测定粒子沉降速度υ，就可算得粒子半径r值。

图3-54　简单的沉降曲线

设沉降前不同半径的粒子均匀地分布在介质中，而且半径相同的粒子沉降速度都相等。若悬浮液中只有一种同样大小的粒子，在沉降天平中测定该悬浮液在不同时间t内沉降在盘中的粒子质量m，做出的m-t曲线（沉降曲线）应该是一条通过原点的直线OA，见图3-54（a）。当时间至t1时，处在液面的粒子亦已沉降到盘上，即沉降完毕，其总沉降量为mc。此后AG即成为平行于横轴的直线。根据盘至液面的距离h和t。可以算出这种粒子的沉降速度：

将此式代入式（3-99），则粒子的半径：

相应的沉降时间为

对于含有两种不同半径粒子的系统，其沉降曲线形状如图3-54（b）所示。在大粒子沉降时总是伴随着小粒子的沉降，OA段反映了大粒子和一部分小粒子的共同沉降，因此斜率较大。至t1时，大粒子全部沉降完毕。此后只剩下较小的粒子继续沉降，因此沉降曲线发生转折，沿AB段上升。至t2时，小粒子也沉降完毕。mc为两种粒子在沉降盘上的总质量。

为了求两种粒子的相对含量，可将线段AB延长，交纵轴于S。OS即为第一种（较大的）粒子的质量，mcS即为第二种（较小的）粒子的质量。因为线段AB是表示只剩下第二种粒子时的沉降曲线，所以其斜率为这种粒子在单位时间内的沉降量。显然，在t2时间内沉降的小粒子质量应为将总量减去小粒子的量，即为第一种大粒子的量，所以Omc-mcS-OS为第一种粒子的沉降量。

实际上所遇到的悬浮液均为粒子半径连续分布的体系，即多级分散体系。其沉降曲线见图3-55。

在某一时间t1，已沉降的粒子质量为m1，按大小可分为两部分。一部分半径大于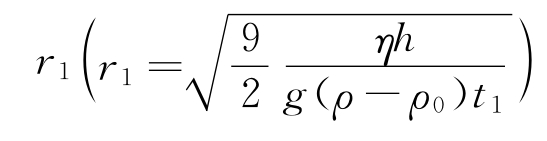的粒子已全部沉降，另一部分半径小于r1的粒子仍在继续沉降。过A点作切线与纵轴交于S1，则m1S1表示半径小于r1的粒子在t1时间内的沉降量，而OS1则表示半径大于r1的粒子全部沉降的量。到t2时，可作B点切线与纵轴交于S2，OS2表示半径大于r2的粒子全部沉降的量，m2S2表示半径小于r2的粒子在t2时间内沉降的量。同理，OS3表示半径大于r3的粒子全部沉降的量等。

图3-55　多级沉降曲线

因此，OS2-OS1=S1S2=ΔS1～2表示半径处于r1和t2之间的粒子的量。同样，S2S3=ΔS1～2表示半径处于r2和r3之间的粒子的量。若沉降总量为mc，则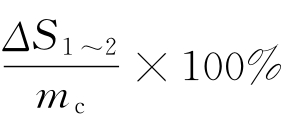表示半径处于r1和r2之间的粒子的量占粒子总量的百分数，以此类推：定义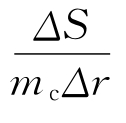为分布函数，以分布函数对r作图，即可得到见图3-56的粒度分布图。

本实验采用带有232接口的电子天平与计算机联用，自动跟踪记录沉降过程中沉降量随时间变化，得到沉降曲线。

图3-56　粒度分布图

3.仪器与试剂

AB104-N电子天平1台；计算机1台；玻璃沉降筒；不锈钢沉降盘；直尺；磁力搅拌器。

滑石粉-去离子水沉降液。

实验装置见图3-57。

图3-57　计算机联用沉降分析实验装置图

1-天平架；2-秤钩连线；3-恒温沉降筒；4-沉降盘

4.实验步骤

（1）沉降高度测量

①将秤盘平稳地挂到电子天平下方的秤钩上，用直尺测量秤盘底部到桌面的距离h0。

②把秤盘放入装有沉降液沉降筒内，测量桌面到沉降液面的距离h1。

③沉降高度h=h1-h0。(www.daowen.com)

（2）将洁净的温度计直接放入沉降液中，测量沉降温度t。

（3）依据沉降温度，记下对应温度t下介质密度ρ与黏度η。

（4）打开“DPZ Release Version.exe”文件，进入程序主界面，单击菜单栏“参数设置”，在弹出“参数设置”窗口设置实验参数，首个采样间隔为1s，总沉降时间为80min，设置完成后，点击“确定”按钮，返回主界面。

（5）用磁力搅拌机充分搅拌沉降液，确保所有粒径的固体颗粒在沉降筒内均匀分布。

（6）关闭搅拌器，消除离心作用后放入沉降盘，迅速将沉降筒移至天平下方，将沉降盘悬挂在秤钩上。（注：挂沉降盘前天平必须先“归零”，务必使沉降盘处于沉降筒中心位置。）

（7）单击“操作”窗口，点击“开始”，计算机开始自动记录时间（t）及相应质量（m），这步操作应在沉降液搅拌停止后20s内完成。

（8）仔细观察计算机屏幕所显示的数据变化是否灵敏且单调增加，如有异常，则实验重新开始。

（9）沉降完成后，点击“导出数据”，保存至D盘。

（10）滑石粉密度测定（图3-58）

图3-58　比重瓶

1-瓶身；2-带毛细管孔的瓶塞；3-盖帽

首先称量洁净干燥的空比重瓶质量为m0，注满蒸馏水后放入恒温槽恒温。15min后用滤纸吸去瓶塞上毛细管口溢出的液体，称得质量m1。倒去水后将比重瓶吹干，放入适量白土称得质量为m2。然后在比重瓶中注入适量蒸馏水，待白土完全润湿后，再将比重瓶注满蒸馏水恒温后，同上操作，称得质量为m3。按下式计算白土的密度ρ。

式中，ρ0为室温下水的密度，kg·m-1。

5.数据处理

（1）沉降总量的计算

在悬浮液中，半径很小的粒子全部沉降完毕需要很长的时间。为此，可用的外推法求得沉降总量，即在沉降曲线的末端取6～8个点，以各个点的沉降量m对应时间t的倒数作图，得一直线，此直线在沉降量轴上的截距相当于总沉降量mc。

（2）沉降曲线的拟合

本实验测得的沉降曲线可用如下的函数表达式描述：

式中，m（t）为沉降粒子的质量（g）；t为沉降时间（s）；a、b、c为与沉降系统性质相关的待定系数：mc为沉降总量。

（3）粒度分布曲线绘制

从式（3-104）很容易看出，当t=0时，m（t）=0，当t→ ∞时，m（t）→mc，这正是本实验所得沉降曲线所要求的。为表征粒子半径大小的分布，依据本实验原理，定义分布函数为

经运算整理可得

分别以分布函数F（r）对r作图，即可得到见图3-56的粒度分布曲线。

（4）计算机处理数据及作图要求

①采用外推法求mc。

②依据沉降曲线的测量值，采用计算机编程拟合沉降曲线，确定式（3-104）中的待定系数a、b、c，分别用相同沉降时间的测量值与拟合值绘制沉降曲线。

③按式（3-102）计算粒子半径r分别为13μm、12μm、11μm、10μm、9μm、8μm、7μm、6μm、5μm、4μm、3μm、2μm的沉降时间。然后在拟合得到的沉降曲线上找到相应的点，求取该点的一阶导数，建立切线方程，得到沉降量轴上各截距（见图3-56中OS1，OS2，…）。根据各截距值分别计算粒子半径为13～12μm，12～11μm，11～10μm，…，3～2μm，2～0μm等不同粒径范围内的相应沉降量ΔS值，计算分布函数，以对Δr得如图3-56中的粒径分布柱形图。也可采用对式（3-104）二次求导得，代入式（3-106）求得分布函数F（r）并对r作图，得粒度分布曲线。

6.思考题

（1）粒子的分布应与温度无关，为什么本实验要在恒温下进行？

（2）为什么要在充分搅拌后才能挂上沉降盘开始测量？若搅拌过猛，在沉降盘下出现气泡，对实验结果有何影响？

（3）若悬浮液中粒子较大以致沉降速度太快，可采用什么措施减慢其沉降速度？