为了避免部分数据增长率为负对回归结果带来的干扰，本章的规模数据全部采用指数形式，为增长率加上1表示；为了缩小与利率数据的差距，利率数据也加1。此外，部分数据只有年度数据，本章将对部分数据采用Quadratic-Match Average方法将年度数据调整为季度数据。

由于是季度数据，比如GDP采用累计值计算的指数（同比），可能存在周期效应，需要通过X12季节调整法调整以后再使用。X12季节调整法是美国商务部人口普查局研究开发的，以移动平均法X11为基础，时间序列{Yt}通过季节调整法，可以剔除趋势循环因素（TC）、季节因素（SF）和不规则因素（IR），以下是四种模型，其中应用最广泛的是乘法模型：

（1）乘法模型：Yt=TCt×SFt×IRt

（2）加法模型：Yt=TCt+SFt+IRt

（3）对数加法模型：log（Yt）=log（TCt）+log（SFt）+log（IRt）

（4）伪对数加法模型：Yt=TCt×（SFt+IRt−1）

进一步的，宏观数据存在明显的时间趋势，采用增长率后不能再进行一阶差分，因为增长率的一阶差分后在经济学上无法解释，因此借鉴一些学者的研究方法，采用H−P滤波方法，将变量中的趋势项剔除，剩余的波动项进行平稳性检验（见表5−2），考察各变量的波动率之间的关系。

表5−2　各指标波动率的平稳性检验(www.daowen.com)

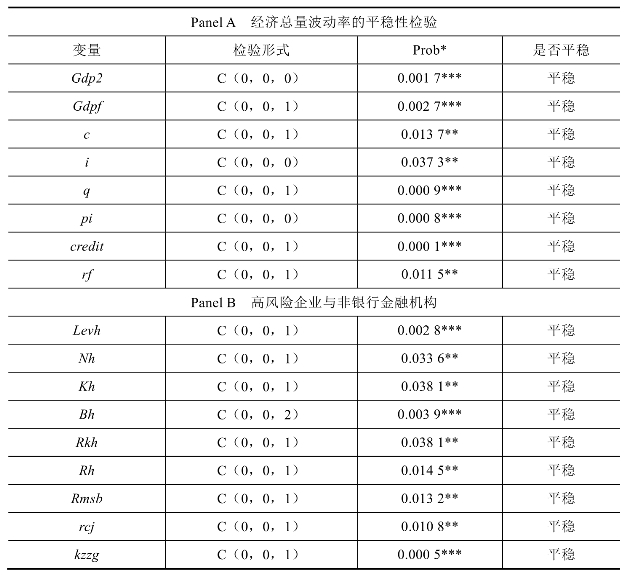
续表

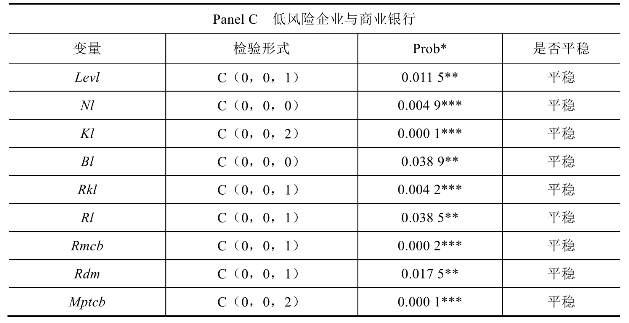
注：***、**、*分别表示在1%、5%、10%的水平上通过统计检验，检验形式（C，T，N）中C代表常数，T代表趋势项，N代表最大滞后阶数。

HP滤波是Hodrick和Prescott在分析美国经济周期时提出的滤波法。该方法将时间序列{Yt}分解为趋势成分和波动成分，有：。损失函数最小问题：。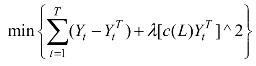

其中，c（L）=（L−1−1）−（1−L）为延迟算子多项式，λ为平滑参数，根据经验，对于年度数据、季度数据和月度数据取值分别为100、1 600和14 400。延迟算子代入上式得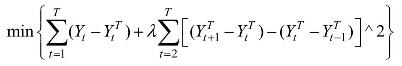：，该式子中第一项反映了波动成分，第二项反映了趋势成分。

由于各个变量的波动率在0附近，所以检验形式全部选择不带常数项和不带趋势项。ADF检验的结果显示各变量的波动率全部平稳，不同的是滞后项不同，大部分是滞后一阶，少部分变量在二阶。