在宏观经济学中，研究多个变量之间的动态关系，需要借助向量自回归（VAR）模型。VAR模型最初由美国学者Litterman、Sargent和Sims等人在20世纪80年代提出的，主要用于替代联立方程结构模型，提高经济预测的准确性。

该模型从数据生成过程的角度对系统内生变量进行解释，充分模拟了系统的动态特征。VAR模型的优点是假设所有变量是内生的，一个变量的值不仅依赖于自身的滞后值，还依赖于其他变量的滞后值。但是VAR模型也存在较多问题，比如VAR模型缺少经济理论的支持，估计参数过多以及变量较多时，合理的滞后阶数如何确定等问题。

VAR（p）模型的基本公式为：

其中，向量yt表示所有的内生变量，Γp是系数矩阵，μt扰动项，服从正态分布。

VAR模型缺少经济理论的支持，无法解释经济的结构，因为VAR模型假设变量之间没有同期影响，因此结构VAR是将结构重新纳入VAR模型中，允许变量之间存在当期影响，SVAR模型的表达式为：

其中，A矩阵为变量当期的结构矩阵。假设A矩阵是非退化矩阵，则有：

令A−1Γp=Φp，A−1μt=εt，则有：

比较S VAR（p）和VAR（p），两者的区别在于扰动项，SVAR是结构扰动项εt。(www.daowen.com)

SVAR模型的优点是变量增加了一些约束条件，但存在待估参数比VAR模型还要多的缺点。

VAR模型和SVAR模型的缺点都是待估参数太多。假设VAR模型中有m个内生变量，变量滞后阶数为p，则待估参数为m（mp+1）。例如，m=5，p=4时，待估参数有125个参数。

产能过剩各个子行业（高风险企业）的杠杆率在2016年以后发生了逆转，整体向下，与“三去一降一补”政策的实施有关；同时，影子银行的规模受到2017年以来严监管的影响，也有下降的态势。为了更加准确的探究2008年全球金融危机以后出现的企业部门杠杆率快速攀升的原因，本书将采取2009—2016年的数据，主要原因：一是由于没有企业向影子银行融资的微观数据，因而采用宏观数据作为替代，但是宏观数据受到监管的影响很大，2016年以后对企业杠杆率和影子银行的外部冲击下，必然会造成经济主体行为的改变，避开这个阶段的数据，只考虑金融机构和企业之间自发形成的融资需求的关系，可以更好地模拟杠杆率快速攀升受到的融资和投资影响的过程。二是国家统计局在2018年以后不再公布分行业的固定资产投资额的累计值，造成高风险企业和低风险企业的资本和资产收益率的缺失，影响模拟过程。三是2009—2016年是杠杆率快速攀升和影子银行大发展的阶段，两者之间的互动关系比较明显。

由于采用2009—2016年的季度数据，时间长度为32期，但内生变量十几个，存在待估参数过多而样本量不足的问题。1986年美国学者Littleman利用贝叶斯向量自回归（BVAR）模型，将所有变量的系数看成围绕其均值的波动，给定系数的分布函数而不是系数的精确数量关系，这样可以利用数据的先验信息得到更准确地系数估计值。大量的研究都表明该方法的预测更加精确，详见朱慧明（2004）学者对该问题的阐述，其系统研究了贝叶斯VAR中的Minnesota共轭先验分布的结构，以及该先验分布下的VAR模型的贝叶斯推断，通过实证分析表明贝叶斯VAR模型的预测效果要优于AR模型和VAR模型。赵进文和丁林涛（2012）对BVAR模型的简化形式为：

其中，B（L）=I−B1L−…−BPLP是滞后算子P的多项式矩阵，yt是n×1阶矩阵，μ是确定的先验值，ut是n×1阶残差项向量，满足Ε（ut）=0和。

BVAR模型对系数设定先验分布，方程i中变量j的滞后期p的系数的先验标准差为：。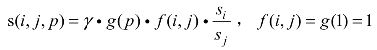

其中，γ为总体紧缩度，表示自变量滞后一期的系数标准差，其取值大小反映了分析人员对先验信息的信心大小的程度，越小代表对先验信息的把握较大；si为变量i自回归方程的残差标准差。g（p）是调和滞后延迟函数，g（p）=p−d，d为衰减系数，表示过去信息的有用程度比当前信息有用程度减少的可能性。f（i，j）是相对紧度函数，表示其他滞后变量相对变量i滞后的权重。