1.商业银行

商业银行的资产负债表公式为：

在式3.1中，资产方，Qt为出售市场价格；表示对低风险企业的债权，包括贷款和购买低风险企业的债券；表示对政府部门的债权，包括贷款和投资国债两种方式，两种资产的利率都为商业银行贷款基准利率。然而，政府融资的目的是宏观调控，作为外生冲击，不是由系统内生决定的，因此在银行资产负债表中简化。At表示商业银行的储备资产，包括现金、法定存款准备金和超额准备金。

是商业银行为影子银行提供资金的两个重要渠道，两个渠道中商业银行都处于主导地位。表示通道业务，通过同业借贷和同业投资方式，以非银行金融机构为通道方，投向银行指定的企业或者置换银行已经存在的贷款和票据，则有商业银行主动购买银行发行的或者其他非银行金融机构发行的资产管理产品，比如计入银行的应收账款类科目。假设存在刚性兑付，表外资产表内化，商业银行通过通道模式和主动购买的资产管理产品，都形成了商业银行对非银行金融机构的债权。因此，对非银行金融机构的债权，存在加权平均利率。其中，表示通道资产占比，表示银行间拆借利率。

负债方，是住户的存款，其利率受中央银行实现物价稳定和经济增长的目标所调控。表示结构性产品，比如银行理财产品、银行存单等，受基准存款利率和银行同业拆借的影响，银行理财收益率，其中，为同业拆借利率对银行理财存款利率的弹性。在刚性兑付下，非保本理财产品与保本理财产品对存款的替代作用相同，类似于“高息揽储”，有。为了简化模型，将两者合并，并且减去准备金，剩下的是银行可以自由支配的存款，利率为两者的加权利率，其中表示影子银行替代银行存款的比例。

借鉴Meeks等（2013）简化的资产负债表形式，将式3.1合并为：

其中，表示银行净值，包括股本和未分配利润两个部分。商业银行经营的目标是实现利润最大化，即实现银行净值最大化。由于商业银行的主要资金来源于存款，通过发行股票募集资金的比例有限，因此银行净值是所有资产收益的累加，包括利息收入和投资收入：

式3.3表示，银行最后一期的净值等于上一期的对低风险企业贷款、影子银行业务和国债的利息收入，扣除支付各类存款的费用。式3.2的第1t−期再乘以，得到：

式3.3减去上式，得到商业银行净值的动态过程：

商业银行关心的是净财富折现后的价值，因为银行家属于家庭成员，在未来时期隐含风险的现金流将按照家庭随机折现因子进行折现。假设在每个时期，银行管理者被新的管理者所取代的概率为σ−1，没有被取代的概率为σ。银行的经营要确保满足储户提现，最优的方式是尽可能地延期支付，直到银行家要求主动退出；当银行管理者被新的管理者所取代时，向储户传递了信号，容易引起储户的恐慌，此时储户对银行净值拥有剩余索取权。因此，第t−1期时银行的价值为，银行的价值最大化目标函数为：

其中，式3.5表示第t−1期的价值等于第t期管理者被替代后支付给储户的银行净值与第t期管理者没被替代时的银行价值之和，根据家庭随机折现因子折现到第t−1期。约束条件式3.7借鉴Gertler和Kiyotaki（2010），银行可能将θc比例的资产用于多样化投资，因此激励相容机制要求银行的特许权价值至少要超过多样化资产的价值。假设银行有机会将一部分资产打包出售卖给家庭部门，ωc表示发行原始贷款的担保比例，当该比例越高时，表明商业银行开展多样化资产的担保将减少，从而导致多样化资产的比例越低。

式3.6和式3.7是一个动态规划问题，需要求助于贝尔曼方程的解法。第t期现值的贝尔曼方程：

假设动态规划问题有内点解，并且值函数连续可微，对xt求导，有：

上式简写为：

代入上式得：

应用贝尔曼（Bellman）方程的解法，价值函数的最值可以表示为微分形式：

其中，分别表示价值函数对贷款、影子银行业务以及存款Dt的偏导数。式3.5和式3.6的最优化求解的拉格朗日函数形式为：

其中，表示拉格朗日乘子。将式3.2和式3.7代入上式，并消除，有：

分别对变量求一阶导数：

式3.8和式3.9相除，消除，得

式3.10整理为：

其中，令参数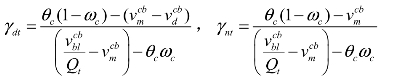

式3.12是最优条件下银行信贷与存款和净值之间的关系，将该条件代入目标函数中，寻找三个偏导数的表达式。将式3.2、式3.11和式3.12代入式3.7中，消除和，得到：

式3.13表示第t期银行的价值是银行存款和银行净资产的线性组合。事实上，家庭储蓄所产生的银行价值为0，因为任何存款水平都产生一个相同的银行持续经营的价值，其结果是整个银行体系可以扩大或者缩小家庭储蓄的任意规模，也就是银行对家庭储蓄能力不产生约束，储蓄量不由银行决定。因此，式3.13第一部分为0，简化为：

整理式3.8，求解出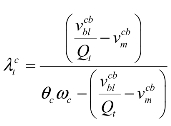代入上式中，得到：(www.daowen.com)

将上式代入式3.5的目标函数中，替换，得：

令，表示银行价值对银行净值的导数值。将式3.2的第t−1期的形式，代入式3.7的第t−1期中，消除，得到的第一个形式；然后将式3.4代入式3.14中，得到的第二个形式，两式相等，有：

式3.15说明第t−1期银行信贷、银行存款和银行净资产的偏导，等于第t期各自实现的收益率乘以银行价值对银行净值的导数值，然后通过家庭折现因子折到第t−1期。整理后可得的系数相等，则可以求解出每个微分的具体表达式为：

式3.16表示第t−1期商业银行贷款变化导致银行价值变动，与影子银行业务变动导致银行价值变动的差距，取决于第t期贷款利率和影子银行收益率之间的差异以及银行价值对银行净值的导数值。式3.17和式3.18分别表示存款变动对银行价值的影响，影子银行业务变动对银行价值的影响都取决于各自的收益率以及银行价值对银行净值的导数值。这表明收益率是联接各个部门的重要桥梁。

2.非银行金融机构

非银行金融机构与商业银行的求解方式类似，唯一不同的是资产负债表形式不同，非银行金融机构不能直接吸收存款，依靠向商业银行拆入资金或者发行资产管理产品，用于向高风险企业发放贷款或购买债券。假设影子银行渠道总负债满足。因此，非银行金融机构资产负债表形式简化为：

其中，Qt为资产出售的市场价格；表示非银行金融机构的净值；表示高风险企业贷款的利率；影子银行总负债的成本为，是银行间拆借利率和发行资管产品的收益率的加权，权重为，表示非银行金融机构从商业银行拆入资金占总负债的比例，即

式3.20表示非银行金融机构的净资产等于向高风险企业发放贷款的收益减去负债的成本。式3.19的第t−1期的形式乘以，得：

将式3.20减去上式，得到非银行金融机构净值的动态过程：

同样的，非银行金融机构的管理者被新的管理者替代的概率是σ−1，替代后债权人拥有非银行金融机构的全部净值，没有被替代时，非银行金融机构的价值为，假设为家庭的随机折现因子。因此，非银行金融机构最大化价值的目标函数为：

其中，θb 表示非银行金融机构的总资产中用于多样化投资的比例，约束条件表示非银行金融机构的价值至少要超过多样化投资资产的价值。

应用贝尔曼方法的解法，非银行金融机构的价值函数的最值可以表示为微分形式：

其中，分别表示价值函数对高风险企业贷款和通过影子银行融资的偏导。

式3.22和式3.23的最优化求解的拉格朗日函数形式为：

其中，表示拉格朗日乘子。将式3.19和式3.24代入上式，并消除，得：

上式对和求一阶导数，得：

式3.25变形为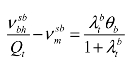：，或者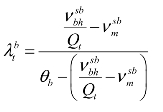

式3.26变形为：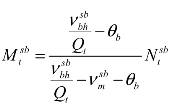

将上面两个变形的式子和式3.19代入式3.24中，消除，得：

将上式代入目标函数式3.22中，得：

令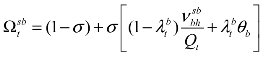，表示非银行金融机构的价值对其净 值的导数值。将式3.19的第t-1期的形式代入式3.24的第t-1期的形式中，消除，得到的第一个形式；然后将式3.21代入式3.27，得到的第二个形式，两式相等，则有：

式3.28说明第1t−期的非银行金融机构的贷款和净资产的偏导数等于第t期各自实现的收益率乘以非银行金融机构价值对净值的导数值，然后通过家庭折现因子折现到第1t−期。的系数相等，则可以求解出每个微分形式的表达式为：

式3.29表示第1t−期非银行金融机构的贷款变动导致的价值变动，与影子银行业务变动导致的价值变差距，取决t期向高风险企业贷款利率和影子银行的融资成本之间的差异以及非银行金融机构的价值对其净值的导数值。式3.30表示非银行金融机构通过影子银行融资的变动对其价值的影响，取决于影子银行融资的成本和的影响。