如图4.13所示，储能设备可以看作由转换及内部存储（认为是理想的）组成。储能转换可类似于能源转换设备建模，其稳态输入、输出功率间的关系为

式中，e_α为储能装置与系统交换功率的效率，这个系数通常取决于功能量流动的方向，即储能装置是储能还是放能（认为Q_α＞0时为储能状态）：

式中，e⁺_α、e^-_α分别为转换的正向、反向能量效率，或称为储能设备的储能、放能效率。根据功率与能量的关系，做一些近似简化有

下面将储能设备加入上一节构建的能量枢纽模型中。能量枢纽可包含多个储能设备，原则上，储能设备可以连接到能量枢纽的输入端，也可连接到输出端。

图4.13 储能设备模型

如图4.14所示能量枢纽，输入端与输出端均置有储能设备。由能量守恒我们可以得到

图4.14 加入储能的能量枢纽模型

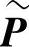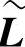图4.13中的阴影部分表示没有储能设备的一组转换设备组件，其功率转换可由式（4.4）表示，将这组转换设备的输入、输出功率分别表示在向量 和 中：

结合式（4.15），有

式中，M包含了输出端所有储能功率，Q包含了输入端所有储能功率，将所有的储能功率等效为一个输出端储能功率向量M^eq：

根据式（4.14），M^eq中的每个元素由两部分组成：(www.daowen.com)

式中，c_αβQ_α将能量枢纽输入端的储能功率折算到了输出端；M_β为输出端的储能功率。将式（4.14）扩展成矩阵形式为

矩阵S称作储能耦合矩阵，它将所有的储能能量衍变为输出功率等效到能量枢纽的输出端。矩阵中的项s_αβ可通过式（4.14）推导。至此，得到包含能源转换及存储设备的完整能量枢纽模型为

现通过图4.15的具体能量枢纽进行式（4.21）推导。

图4.15 能量枢纽示例

构建此能量枢纽的耦合矩阵为

储能设备交换的功率为

现在式（4.16）可构建为

接下来将输入输出端的储能功率转换为等效的能量枢纽输出功率，即

得到储能耦合矩阵

最后，根据式（4.21）构建该能量枢纽模型为