由于综合指数涉及的经济现象较为复杂，经济现象指数化指标之间不能直接相加和对比，因此要想将复杂经济现象的指数化指标进行对比，首先必须讲清楚同度量因素的问题。

（一）同度量因素

1.同度量因素的概念

为了解决复杂经济现象的指数化指标不能直接相加的问题，必须引入一个媒介因素，使其转化为价值总量形式之后可以相加对比，该因素称为同度量因素。

2.同度量因素的确定

同度量因素要在研究对象的经济变量关系中寻找。例如，研究某地区商品销售价格变动程度时，通常的经济关系：销售价格×销售量＝销售额。众多不同种类的商品的单价不能直接相加对比，而如果通过引入销售量，与单价相乘可以使众多不同种类商品的单价转化成相同度量单位的销售额，所以，这里的销售量就是同度量因素。当然，同样的思路，也可以在研究销售量的变动程度，选择销售的价格做其同度量因素，即它们互为同度量因素。当然，同度量因素在起到媒介作用的同时，也有权衡轻重的作用，也可称为权数。

3.同度量因素时间的确定

上面讲到，销售价格和销售量互为同度量因素，但是销售价格与销售量都有基期和报告期之分，究竟是选择基期还是报告期，因此，同度量因素还有一个时间的确定问题。事实上，有时还可以固定在某个具有代表性的特定时期。

（1）将作为同度量因素的各变量值固定在基期来计算指数，这是最重要的一种综合指数方法，其制定者是德国经济统计学家拉斯贝尔斯（E.Laspeyres），因此又称为拉氏指数。

（2）将作为同度量因素的各变量值固定在报告期来计算指数，这是最重要的一种综合指数方法，其制定者是德国经济统计学家帕舍（H.Paasche），因此又称为帕氏指数。

（3）将作为同度量因素的各变量值固定在某个具有代表性的特定时期来计算指数。这一方法，同度量的选择具有很大的灵活性，既不受基期也不受报告期的限制，使得指数的应用相当广泛。采用特定时期的权数加权所计算的指数，不仅便于分析指数的长期走势，也便于环比指数和定基指数之间的换算。

（二）综合指数的编制

综合指数是总指数的一种形式，它是两个综合的总量指标对比形成的指数。也就是说，综合指数是对复杂现象的两个时期的总量进行动态比较所形成的指数。综合指数有两个指标，即质量指标综合指数和数量指标综合指数。现分述如下。

1.质量指标综合指数的编制

【例8－1】下面以物价指数为例，说明综合指数中质量指标综合指数的编制方法。

设某商店小麦、洗衣机、摩托车三种商品价格和销售量资料如下表。

表8－2　商品价格和销售量表

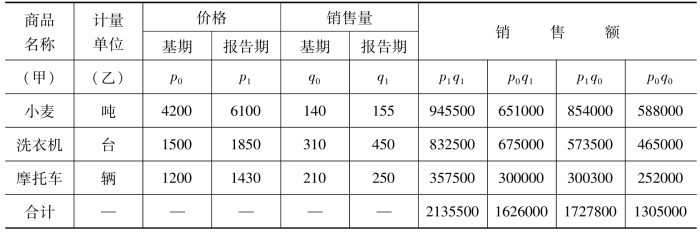
有关符号的意义说明如下：

k表示个体指数，¯k表示总指数，p0表示基期价格，p1表示报告期价格，q0表示基期销售量，q1表示报告期销售量。

现在，想了解全部商品价格的变动情况。我们知道，将不同时期的各种商品价格对比可以看出商品价格在不同时期的变化。因此，由上面的资料，可以计算小麦、洗衣机、摩托车三种商品的个体价格指数：

计算结果说明，小麦价格上涨了45．23%，洗衣机价格上涨了23．33%，摩托车价格上涨了19．17%。

但是，上面这些个体指数只是反映了每一种商品价格变动的情况，却没有反映这个商店三种商品价格总的变动情况，而反映某商店商品总价格变动正是我们在经济管理中所需要的，因此，就必须计算反映价格总变动的指标——价格综合指数，即找出两个时期的价格总和，然后把两个时期的价格总和进行对比。

（1）拉氏质量综合指数是指将作为同度量因素的各变量值固定在基期来计算指数。一般计算公式：

【例8－2】根据表8－2的数据用上面公式可得：

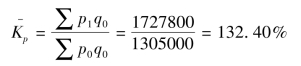
∑p1 q0－∑p0 q0＝1727800－1305000＝422800（元）(www.daowen.com)

计算结果表明，三种商品价格指数为132．40%，报告期比基期平均上涨了32．40%，由于价格上涨，使商店多收入了422800元。

（2）帕氏质量综合指数是指将作为同度量因素的各变量值固定在报告期来计算指数。一般计算公式：

【例8－3】根据表8－2的数据用上面公式可得：

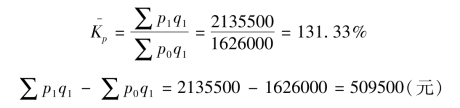
计算结果表明，三种商品价格指数为131．33%，报告期比基期平均上涨了31．33%，由于价格上涨，使商店多收入509500元。

对于上面的两个公式，究竟应该采用哪个呢？这要看研究目的及掌握的资料情况来确定。例如，如果我们的目的是研究价格变化的实际经济效果，则使用帕氏公式计算是比较合理的，因为它反映的是商店销售当前的商品数量时，由于价格的变动使之多收入的数额，它的现实意义比较强，而拉氏公式则无现实意义，因此，在我国多数人主张，在计算质量指数时，使用报告期的数量指标作为同度量因素，简称“质报”。这也是为人们所常用的方法，即

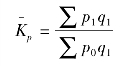
2.数量指标综合指数的编制

【例8－4】下面以销售量指数为例，说明综合指数中数量指标综合指数的编制方法。

仍用上述的例题，假设某商店小麦、洗衣机、摩托车三种商品价格和销售量资料，现在我们想了解该商店销售量的变动情况。

我们知道，将不同时期的各种销售量对比可以看出销售量在不同时期的变化，因此，由上面的资料，可以计算出小麦、洗衣机、摩托车三种商品的个体销售量指数。

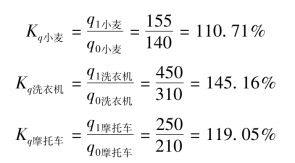
计算结果表明，小麦的销售量增加了10．71%，洗衣机的销售量增加了45．16%，摩托车的销售量增加了19．05%。

但是，上面的这些个体指数只是反映了每种商品销售量的变动，却没有反映这商店三种商品销售量总的变动情况，要反映三种商品销售量总的变动情况，就必须计算商品销售量综合指数，即找出两个时期的销售量总和，然后把两个时期的销售量总和进行对比。

（1）拉氏数量综合指数是指将作为同度量因素的各变量值固定在基期来计算指数。一般计算公式：

【例8－5】利用表8－2的数据用上面公式，得

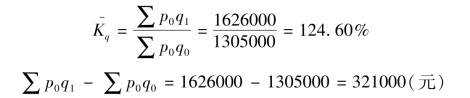
计算结果表明，三种商品销售量平均上升了24．60%。由于销售量上升，使商品销售额增加了321000元。

（2）帕氏数量综合指数是指将作为同度量因素的各变量值固定在报告期来计算指数。一般计算公式：

【例8－6】利用表8－2的数据计算得：

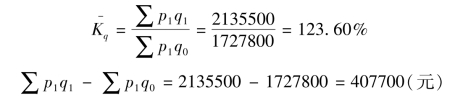
计算结果表明，三种商品销售量平均上升了23．60%。由于销售量上升，使销售额增加了407700元销售收入。

通过计算可以看出，用两种公式计算的销售量总指数是不同的。那么到底使用哪个公式更科学呢？这也要看分析研究的目的和所掌握的资料情况来确定。

一般来说，观察数量指标的变动以不包括价格变动的因素为好，因此，我国多数人主张，在计算数量指数时，使用基期的质量指标作为同度量因素，简称“数基”。这也是人们常用的方法，即

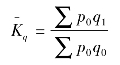
从经济内容出发，兼顾到指数体系，在同度量因素的固定上，有一个约定俗成的做法：即分析质量指标的变动时，它的同度量因素为数量指标，并固定在报告期；分析数量指标的变动时，其同度量因素为质量指标，并固定在基期。