（一）长期趋势的意义

所谓长期趋势是指客观现象在一个相当长的时期内沿着一个方向持续发展变化的现象。现象的长期趋势是客观存在的，是现象发展变化过程中的主要倾向。认识了长期趋势，就可把握住现象发展变化过程的基本特点，并可据以预测现象未来的状况。

（二）测定长期趋势的方法

长期趋势有两种基本形式，一种是直线趋势，另一种是非直线趋势（即曲线趋势）。后者又有不同的具体形态。

为了分析现象发展变化的长期趋势，必须从原有时间数列中，消除基本因素以外的各类因素的影响，这项工作叫时间数列修匀（或动态修匀）。也就是测定现象发展变化过程中的长期趋势。此类方法很多.下面着重介绍几种常用的方法。

1.时距扩大法

时距扩大法，就是把原时期数列各指标所包含的时间范围扩大，以消除原动态数列由于时期较短而受偶然性因素影响所引起的波动，从而明显地表现出现象发展的趋势。

【例7－14】表7－18为某厂4月份上半月产量数字。

表7－18　4月份上半月每天产量　单位：万件

这个数列所表现的产量增长趋势，出于时间相隔很短，出现上下波动，显得模糊不清。现采用时矩扩大法，把上表资料由一日扩大到五日。

表7－19　4月份上半月产量的时距扩大表　单位：万件

如上表就明显地看出该厂4月份上半月产量呈上升趋势。

时期的扩大程度应根据研究现象的性质和实际情况而定。时期过大，会掩盖现象发展的具体过程；时期过小，又不易消除现象发展过程中受偶然因素影响所引起的波动。各个时期的数字才可以进行比较，从而表明现象发展的总趋势。

2.序时平均法

序时平均法，就是对原动态数列进行加工整理时，将时期数列的时期或时点数列的间隔扩大，并计算出各个序时平均数，编成一个新的动态数列，以反映现象在各个时期内一般水平的变动情况，从而更明显地揭示现象发展变化的趋势。

【例7－15】某厂2011年各月的职工人数资料如下表。又知2012年1月初人数为168人。计算各季平均人数。

表7－20　某厂2011年各月的职工人数资料

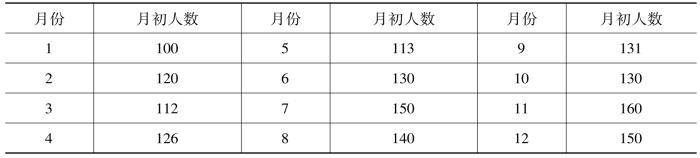
第一季度平均人数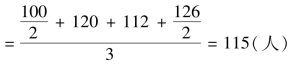

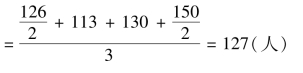
第二季度平均人数

第三季度平均人数＝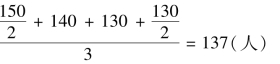

第四季度平均人数＝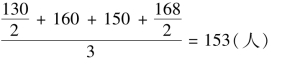

将序时平均数编成动态数列。如下表7－21所示。

表7－21　某厂2011年季度平均人数

从这个动态数列中就明显地看出该厂在2011年人数呈不断上升趋势。

序时平均数，不仅适用于时点数列的修匀而且也适用于时期数列的修匀；另外，时期或间隔的长度可以相等，也可以不等。

3.移动平均法

移动平均法，就是将原动态数列的时期扩大，用逐项移动的方法计算扩大时期以后的序时平均数，边移动边平均，就得到一个新的序时平均数动态数列，从而呈现出现象发展的趋势。

例如将前面表7－19的资料的时期扩大为五天，计算第一天到第五天的平均数，作为第1～5天的代表值（排列位置上对准第三天），计算第二天到第六天的平均数作为第2～6天的代表值（排序位置对准第四天）。照此移动下去，直至最后一个数据为止。

必须注意，移动平均法所取平均单位项数的多少，应视资料的特点而定。如果动态数列有周期性规律性可循，则应以循环周期的长度作为移动平均的时间长度，如一年（季节变动）或若干年（循环变动）移动平均。因为只有这样，才能有效地消除季节变动和循环变动。从而较准确地反映长期趋势；如果现象的变化不存在周期性，则最好采用奇数项（如3、5、7等）移动平均。因为这时各区间的中点正好落在原数列的各中间项上。保持了资料的对口，只需经一次移动平均就可求得趋势值。但若采用偶数项移动平均，所得数值与原指标数值在时间上错动了半年，为了校正，需在第一次偶数项移动平均数的基础上，进行第二次二项移动平均。

表7－22　某公司产量的五项移动平均表　单位：百件

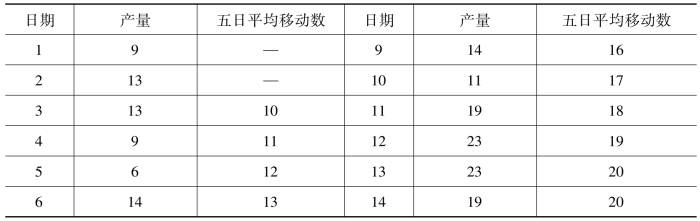
续表：

【例7－16】根据表7－22的资料，其四年移动平均数计算过程如下：

表7－23　某空调厂新世纪以来的年空调产量　单位：台

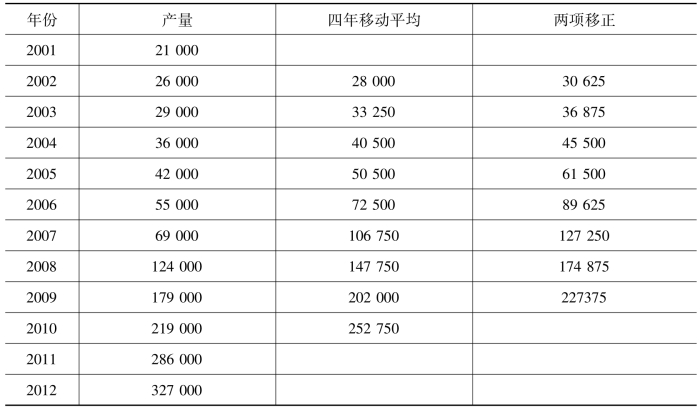
移动平均后所得的修正数列，较原数列项数要少。而且，移动平均的时间长，减少的项数就越多。所以，为了准确地分析长期趋势，计算移动平均数的时间不宜过长，以免给其后的动态分析带来不便。

4.数学模型法

数学模型法就是用一个数学方程来代表现象的长期趋势。这种代表现象长期趋势的数学方程，叫做趋势方程。

一个趋势方程能否准确代表现象的长期趋势，取决于以下两个问题的正确解决：第一，选好趋势方程的形式；第二，选好确定趋势方程式中有关参数的方法。

趋势方程依据现象长期趋势的表现形式不同，可归纳成直线趋势方程和曲线趋势方程两大类。其中，曲线趋势方程，又可进一步分成二次曲线趋势方程、三次曲线趋势方程、指数曲线趋势方程等等。下面先介绍直线趋势方程。

（1）直线趋势方程。直线趋势方程的形式为：

yc＝a＋bx

式中，yc代表现象的长期趋势值；x代表时间顺序；a、b为两个待定参数。

求出参数a、b最常用的方法是最小平方法。

最小平方法要求现象的实际值与其相应趋势值离差的平方和达到最小值。用符号表示则：∑（y－yc）2＝最小值

将yc＝a＋bx代入后，根据求极值原理，分别对a、b求偏导数，可得求解a、b参数的方程组：

设：Q＝∑（y－yc）2＝∑（y－a－bx）2

求a和b的一阶偏导数，令其等于零。

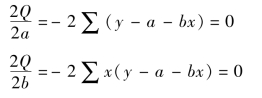
整理得：

∑y＝na＋b∑x

∑xy＝a∑x＋b∑x2

这个方程组的求解公式是：

【例7－17】以某行业固定资产额X与产品产量Y来说明之（数据见表7－24）。

将表中各有关数值直接代入参数求解公式：

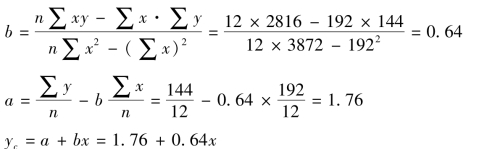(www.daowen.com)

用最小平方法拟合的直线趋势方程表明：随着固定资产额每上升一个单位，产品产量会上升0．64个单位。

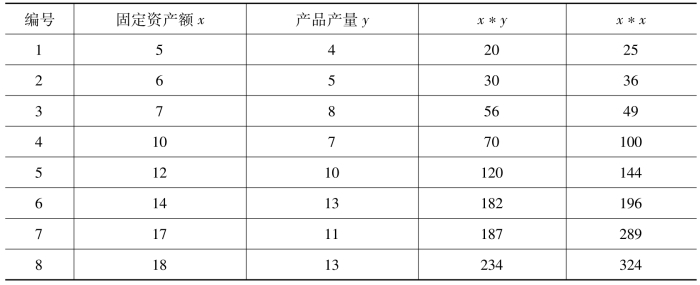
表7－24　直线趋势拟合最小平方法计算表

续表：

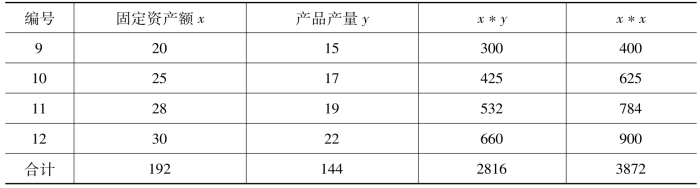
最小平方法因其数学依据较为科学而使其拟合的结果较为精确，对时间数列原有数据具有较高的代表性，但其计算过程较繁。在日常工作中，可用简捷法求出a、b的数值；

首先令∑x＝0，则a、b的求解方程为：

∑y＝na

∑xy＝b∑x2

于是：

为了得到∑x＝0，可对原时间数列的时间顺序数做如下假设：如果时间数列是奇数项，则令其中间一期为原点，由此x为－3、－2、－1、0、1、2、3…，∑x＝0；如果时间数列是偶数项时，则令x为－5、－3、－1、1、3、5、…，这样∑x＝0。

（2）曲线趋势方程。有些社会经济现象的发展趋势，并不是逐期等量增加或减少，而是呈曲线趋势。这时就要用适当的曲线方程来反映其发展趋势。曲线趋势方程种类很多，其中主要有二次曲线、指数曲线等。

①二次曲线趋势方程。二次曲线趋势方程的一般形式为：

yc＝a＋bx＋cx2

式中：y代表现象的长期趋势值，x代表时间顺序，a、b、c为三个待定参数。

求参数a、b、c时，一般用最小平方法，最小平方法的数学要求是：

∑（x－yc）2＝最小值

则yc＝a＋bx＋cx2代入上式，按要求极值原理，分别对a、b、c求偏导数，得求解a、b、c数的方程组为：

∑y＝na＋b∑x＋c∑x2

∑xy＝a∑x＋b∑x2＋c∑x3

∑x2 y＝a∑x2＋b∑x3＋c∑x4从上述方程组求解a、b、c各值，计算过程颇为烦琐，可用简捷法计算。

如令∑x＝0，则∑x3＝0，这时，求解的标准方程组可简化为：

∑y＝na＋c∑x2

∑xy＝b∑x2

∑x2 y＝a∑x2＋c∑x4

由此可得：

【例7－18】现以2001～2011年某市某种家用电器产量为例说明之（见表7－25）。

据此，可求出a、b、c三个参数：

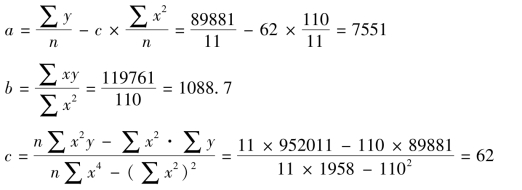
表7－25　二次曲线趋势拟合最小平方法计算表

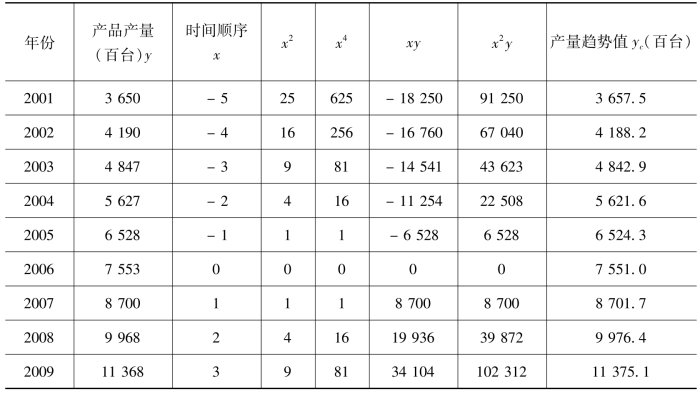
续表：

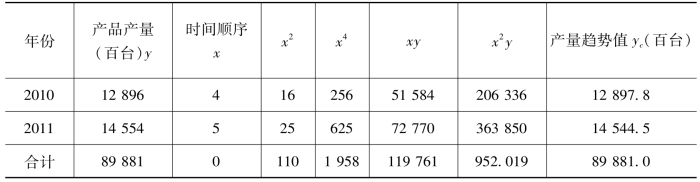
则　yc＝7551＋1088．7x＋62x2

将x＝5、－4、…、4、5代入上列趋势方程，求得现象的长期趋势值（见表7－25的最后一栏）。

二次曲线趋势方程，适用于分析二级增减量大致相等的现象。

②指数曲线趋势方程。指数曲线趋势方程的一般式是：

yc＝abx

式中，yc、a、b的意思同前。

指数曲线趋势方程，适用于分析环比增长速度大致相等的现象。

指数曲线趋势方程中参数a、b的求解，可用半数平均法或最小平方法。但为了求解的方便，可用对数原理将指数曲线趋势方程转化为直线趋势方程：

lg yc＝lg a＋x lg b

如果用最小平方法拟合，则lg a、lg b的求解方程组为：

∑lg y＝n lg a＋lg b·∑x

∑x lg y＝lg a·∑x＋lg b·∑x2

用简捷法求解时令∑x＝0，则

∑lg y＝n lg a

∑x lg y＝lg b·∑x2

解上列方程组，得：

【例7－19】现以我国商业部门2002～2012年社会零售额的资料为例说明之（见表7－26）。

由表7－26资料得：

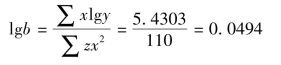
∴lg yc＝3．2910＋0．0494x

则yc＝1954．3×1．12x

表7－26　指数曲线趋势拟合最小平方法计算表

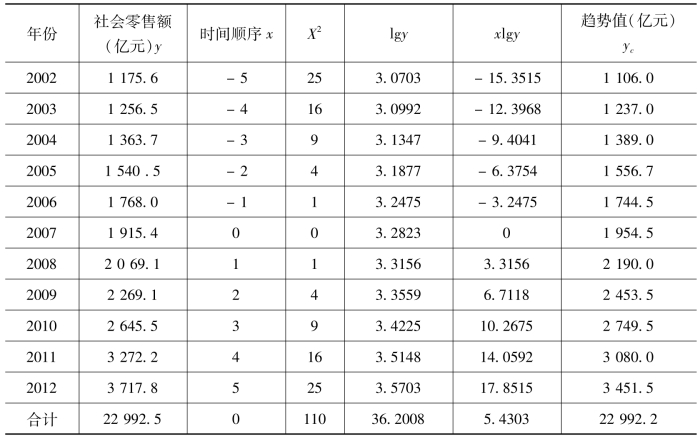
将x的不同取值代入该方程，可求得社会零售总额的趋势值（见表7－26的最后一栏）。