（一）平均发展速度和平均增长速度的意义

平均发展速度是各期环比发展速度的序时平均数，用以说明现象在一段时间内平均发展变化的程度。平均增长速度是各期环比增长速度的序时平均数，用以反映现象在一段时间内平均增长变化的程度。平均增长速度不能根据各期的环比增长速度直接计算，而要通过平均发展速度减去1来求得。两者的关系为：平均增长速度＝平均发展速度－1。

平均速度指标在统计分析中有着广泛的应用，它可以用于编制和检查计划，对比不同时期、不同国家或者地区经济发展变化，进行推算和预测等。

（二）平均发展速度的计算方法

平均发展速度通常采用几何平均法和方程法计算。

1.几何平均法

根据上述的平均发展速度的定义，对若干个环比发展速度求序时平均数，就需要用几何平均的方法，设以xi（i＝1，2，…，n）表示各期环比发展速度，以表示平均发展速度，则有

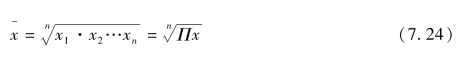
式中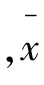代表平均发展速度；x1，x2，…，xn代表各环比发展速度；n为环比发展速度的个数；Π为连乘符号。

【例7－12】根据我国“十五”时期工业总产值环比发展速度，计算“十五”时期我国工业的平均发展速度。资料见表7－17所示。

表7－17　我国“十五”时期工业发展速度

将表中资料代入公式得：

计算结果表明，“十五”期间我国工业发展速度（用工业总产值为计算指标）平均达到110．7%。

由于各期环比发展速度的连乘积等于定基发展速度（总速度）（定基发展速度用R表示）：

x1·x2…xn＝R

故

又因：R(www.daowen.com)

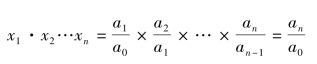
故

例如，利用表7－15的资料，计算我国“十五”时期国民收入的平均发展速度时，就宜选用公式（3）：

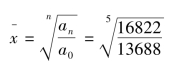
上述三个公式的应用，可视掌握资料的情况而定。在实际经济工作中，只用一种方法计算就可以了，若以上资料都掌握，通过以上计算可以看出用总速度公式计算最简便。可见，应用几何平均法计算平均发展速度的基本思想是，从最初水平出发，每期按平均发展速度发展，经过n期后将达到最末水平。该方法的特点是考察期末水平，中间水平无论如何变化对平均发展速度的计算结果都没有影响。因此该方法也称为“水平法”。在实际应用中，如果关心的是现象在最后一期应达到的水平，采用几何平均法计算平均发展速度比较合适。

需要特别指出的是，平均增长速度不能根据各期的环比增长速度直接计算，而要通过平均发展速度减去1来求得。两者的关系为：平均增长速度＝平均发展速度－1。

例如，已知某地区2004～2010年国内生产总值多年的增长速度分别为4．8%、9%、8．8%、8．1%、11．6%、16．1%，要计算这一地区2004～2010年国内生产总值平均增长速度就不能直接用各期增长速度计算，而应该先将各期增长速度加上100%，变成各期环比发展速度，然后再按照平均发展速度计算方法，计算其平均发展速度，最后运用平均发展速度与平均增长速度之间的关系，计算出平均增长速度。具体过程如下：

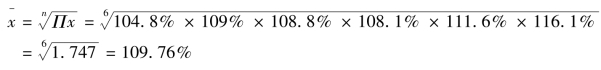
平均增长速度为：109．76%－100%＝9．76%

2.高次方程法

高次方程法亦称累计法，其基本思想是：从最初水平出发，按平均发展水平速度发展，计算出各期发展水平的总和，等于相应各期实际发展水平的总和，所以叫累计法。即：

将上式整理得：

上述等式实质上是个高次方程，其中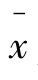为未知数，是常数项。将a0，a1，…，an的数值和相应的n代入上式，解高次方程所得的正实根，即为所求的平均发展速度。由于该方法计算平均发展速度的特点是考察各期水平的累计总和，因此该方法亦称累计法。在实际应用中，如果侧重于研究现象在一段时间内各期发展水平的总和。如累计固定资产投资完成额、累计毕业生人数等，采用高次方程法计算平均发展速度比较合适。有关高次方程法求解出高次方程是比较复杂的，在实际工作中往往利用事先编好的《平均增长速度查对表》应用，这里我们不作简述了。

【例7－13】根据表7－18中的资料，用高次方程式法计算“十五”期间我国各年的国民收入的平均发展速度为：

解得

计算表明，“十五”期间我国国民收入的年平均发展速度为110.9%。