（一）发展水平

发展水平，又称发展量，它是指在时间数列中每个指标数值反映社会经济在不同时期或时点所达到的总量，所以称为发展水平。发展水平一般表现为绝对数。它是表明社会经济现象在各个时期所达到的规模和发展水平的重要指标，是计算其他时间数列分析指标的基础。

发展水平指标，一般属总量指标，也有平均指标和相对指标。发展水平通常用a表示，由于在时间数列中所处的位置不同，各期发展水平分别表示为：

a0，a1，a2，a3，…，an－1，an

按照发展水平在时间数列中的位置不同，可以区分为最初水平（即初期水平，用a0表示）和最末水平（即末期水平，用an表示），其余中间各项指标数值叫做中间水平。

根据发展水平在动态分析中的作用不同，通常把被研究时期的水平叫报告期水平（或计算期水平），把作为比较基础那一时期的水平叫做基期水平。这些不同的水平指标，都不是固定不变的，由于研究目的不同，它会随着时间的推移而相应改变，本期的报告期水平，可能是下一期或将来的基期水平；本数列的最末水平，可能是下一个数列的最初水平等等。见表7－6所示。

表7－6　“十一五”期间国内生产总值表

从表7－6可以看出我国国内生产总值在“十一五”时期所达到的水平。

a0为184937．4亿元，是“十一五”时期前一年的水平，为最初水平。a5是最末水平，表明“十一五”时期最后一年国内生产总值。如果对比2010年和2005年两年国内生产总值的发展水平，则a5＝401202（亿元）为报告期水平。a0＝184937．4（亿元）为基期水平。

（二）平均发展水平

1.平均发展水平的概念

时间数列中各期的发展水平加以平均而得到的平均数叫做平均发展水平，也叫“序时平均数”。它和一般平均数有共同之处，都是将研究社会经济现象的个别数量差异抽象化，概括地反映社会经济现象的一般水平。但两者也有差别，一般平均数是将同一时期的标志总量与总体单位总数对比求得，是总体各单位之间标志值的平均，从静态上说明社会经济现象的一般水平，故又称静态平均数。而平均发展水平则是将不同时期的指标数值加以平均而求得，是时间数列中各时间单位之间发展水平的平均，从动态上说明社会经济现象在某一段时间内的一般水平，故又称动态平均数。

2.计算方法

计算平均发展水平的方法依据数列中指标的性质不同而略有不同。它既可以用总量指标时间数列计算，也可以用相对指标时间数列和平均指标时间数列计算。其中，总量指标时间数列计算序时平均数是最基本的。

（1）根据总量指标动态数列计算序时平均数。

①由时期数列计算序时平均数，只需采用简单算术平均法即可。此法用公式表示如下：

设以表示平均发展水平（下同），则

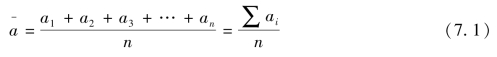
【例7－1】已知某建设项目2008～2012年的投资额资料，见表7－7所示：

表7－7　某建设项目2008～2012年的投资额

则平均每年投资额：

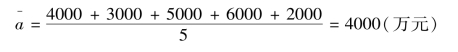
②由时点数列计算序时平均数。

（A）以日计算的时点资料，如果是时间间隔相等的连续时点资料可用简单算术平均法求序时平均数。计算公式为：

例如，已知某施工企业一个月内每天的工人人数，要计算该月内每天平均工人数，可将每天的工人数相加，除以该月的日历日数。

（B）以日计算的时点资料，如果是时间间隔不等的连续时点资料，要用加权算术平均法求序时平均数。计算公式如下：

设f表示时间间隔长度，则

【例7－2】某建筑施工企业8月1日至8月11日职工人数均为1000人，8月12日至8月20日职工人数增加到1100人，8月21日至8月31日职工人数又减少到1050人，则该施工企业8月份职工平均人数为：

（C）以月度、季度、年度初或者未登记的初期末的间断时点资料，如果是时间间隔相等的间断时点资料，可用首尾折半法计算。计算公式为：

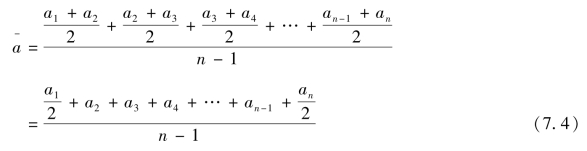
即其序时平均数为最初水平的一半加上中间水平，再加最末水平的一半，然后除以项数减1，故称“首尾折半法”，也可用下列语言描述：首尾折半加中间各项之和再除以项数减1。

以表7－8的资料为例，说明计算公式的由来。

表7－8　某生产企业2012年三季度各月末库存商品额　单位：万元

第一步：用“两两移动平均法”先计算各时点区间（月）的平均数：

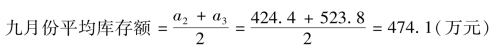
第二步：用“简单算术平均法”先计算全季度的平均数：

上述计算中的两个步骤可以合并为一步：

上述计算过程用公式表示如下：

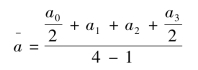
用上式计算序时平均数有两个假定条件：①现象在两点之间的数量变动是均匀的；②各时点的上期期末数即为本期期初数。例如，六月末商品库存额为325．2万元，这325．2万元同时也是七月初的商品库存额。但实际上现象的变动及数量关系并非完全如此，故用这个公式计算的结果，只是个近似值。

如间隔相等的时点资料，时点取在各期中点，则可用“简单算术平均法”直接计算。

（D）以月度、季度、年度初或者末登记的期初或期末的间断时点资料，如果是时间间隔不等的间断时点资料，可用加权首尾折半法计算。计算公式为：

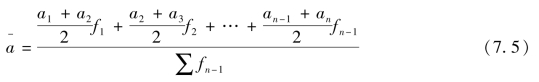
【例7－3】　表7－9为2011年某城市房地产中介数量变动情况。

表7－9　2011年某城市房地产中介数量变动情况

根据该表资料计算该城市2011年房地产中介数量的平均数：

全年平均数

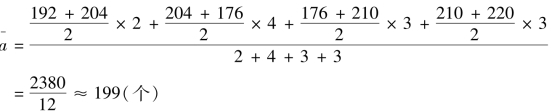
上面所介绍的五个公式是关于总量指标时间数列求序时平均数计算的基本公式。其他两种时间数列（相对数时间数列和平均数时间数列）的序时平均数计算就是这五个基本计算公式的具体运用。

（2）根据相对数指标时间数列计算序时平均数。

由于相对数指标时间数列一般都是由两个有联系的总量指标时间数列相对比而计算出来的，分为差比相对数和商比相对数，差比相对数时间数列的序时平均数在后面平均增长量中介绍，这里先介绍商比相对数序时平均数的计算。其序时平均数相应地通过分子数列的序时平均数和分母数列的序时平均数相对比来计算。可用符号表示如下：

设ai为相对数时间数列的子项，bi为相对数时间数列的母，ci为相对数时间数列的指标值，则

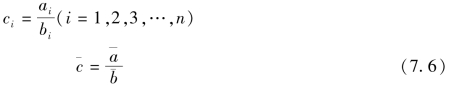(www.daowen.com)

（7．5）式为相对数时间数列序时平均数的基本公式，其具体应用过程，随被研究现象的性质和掌握资料的情况不同而异。现就三种常见的情况加以说明。

①由两个时期数列对比形成的相对数时间数列求序时平均数。此时ai和bi都是时期数列，故分子和分母的序时平均数和都是用“简单算术平均法”计算，用公式表示为：

【例7－4】某企业2011年商品产值计划完成情况资料如表7－10所示。

表7－10　某企业2011年商品产值计划完成情况　单位：万元

计算2002年季度商品产值计划平均完成程度。

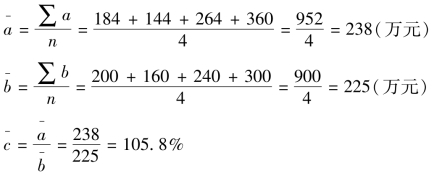
即该企业2011年四个季度商品产值计划平均完成程度为105．8%。在这种情况下，显然：

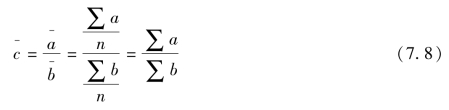
利用表7－10资料计算，得：

又因为所以

则上式可变形为：

利用表7－10资料计算得：

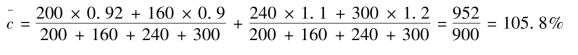
或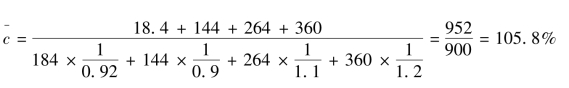

上述三个公式已用实例证实其计算结果完全相同，实际工作中可根据所掌握的资料情况来选择应用。

②由两个时点数列对比而成的相对数时间数列求序时平均数。

由于时点数列有连续和不连续之分，间隔有相等和不相等之别，同时存在分子和分母的情况相同和不同，所以理论上存在十六种情况。下面仅以分子和分母相同的情况为例：

（A）由两个连续（以天为计算单位）时点数列对比而形成的相对数时间数列求序时平均数，其基本公式仍然是：

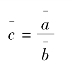
这里的a和b都是连续时点数列，具体有：

每天资料：

间隔若干天的资料：

（B）由两个间隔相等的间断（以月、季、年为计算单位）时点数列对比而成的相对数时间数列求序时平均数，计算公式为：

同理，以a＝bc及代入上式，也可得出另外两个变形计算式。即

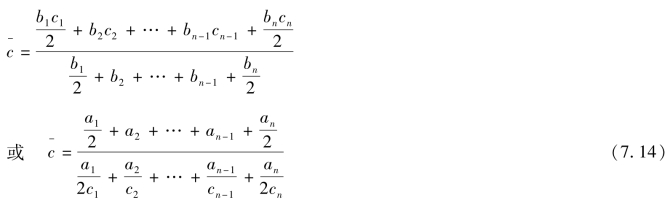
【例7－5】某生产企业职工人数及非生产人员资料如下：

表7－11　某企业职工构成情况变动表　单位：人

试求第一、二季度非生产人员平均比重。

根据本例资料特征计算序时平均数为：

第一季度非生产人员平均比重

第二季度非生产人员平均比重

上述计算结果表明，第二季度非生产人员在全部职工人数中的比例比第一季度小，说明企业在人员分配上注意向生产一线倾斜，有利提高全员劳动生产率。

（C）由两个间隔不等的间断时点数列对比而成的相对数时间数列求序时平均数，计算公式为：

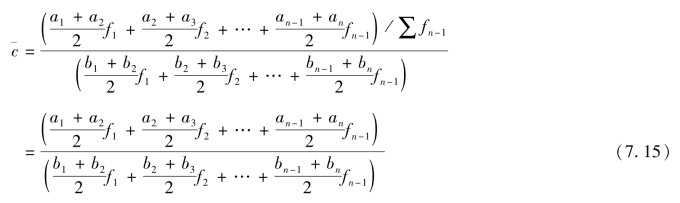
③由一个时期数列和一个时点数列对比而成的相对数时间数列求序时平均数设时期数列为a1，a2，a3，…，an，时点数列为b1，b2，b3，…，ba，则

其中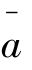为时期指标动态平均数，计算比较简单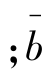为时点指标时间平均数，要根据掌握的资料用相应的公式计算。理论上，这种情况下，有四个计算公式。下面仅以时点指标的序时平均数的计算是采用首尾折半法为例。

【例7－6】用表7－12的资料计算该厂工人一季度月平均劳动生产率。

表7－12　某厂一季度各月工人生产情况

工人第一季度月平均劳动生产率

由于时期指标各月的指标数值加总后表示更长时期的总量，故上例还可以计算整个第一季度的劳动生产率，即

（3）根据平均数时间数列计算。

平均数有总体单位平均数（静态平均数）与序时平均数（动态平均数）之分。这两种性质各异的平均数的计算方法也不同。

总体单位平均数实际上是总体标志总量与总体单位总量对比所得。因而，其序时平均数与静态相对数的序时平均数计算方法一样，用总体标志总量的序时平均数（即时期数列序时平均）与总体单位总量的序时平均数（用时点数列的各种序时平均法计算）对比而得，无须赘述。

至于由序时平均数进一步求其序时平均数，只需用“简单算术平均法”。如表7－13中各月的流动资金平均结余额，便是一序时平均数时间数列。

表7－13　某厂2012年第一季度结余情况

第一季度月平均流动资金结余额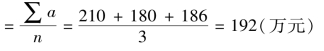

如果计算对象中每个平均数指标的时间长度不同，则需要用加权算术平均法计算：