（一）拟合优度的检验

多元线性回归分析中，普通最小二乘法所保证的最好拟合，仍是同一个问题内部的比较，比较不同问题之间的优劣，仍需要检验拟合优度。在多元线性回归分析中，总离差平方和的分解公式仍然成立。因而上一节定义的判定系数的计算公式（6．6）在这里仍成立。

但是，从（6．6）式可以看出，拟合优度的大小取决于残差平方和SSE在总离差平方和SST中所占的比重。在样本容量一定的条件下，总离差平方和与自变量的个数k无关，但是当自变量的个数增加时，可能会使预测误差变小，从而减少残差平方和（至少不会增加），这样拟合优度是自变量个数k的非递减函数。在一元线性回归模型中，不同的模型都仅含有一个自变量，如果使用的样本容量也一样，判定系数便可以直接作为评价拟合优度优劣的尺度。然而，在多元线性回归模型中，不同的模型所包含的自变量个数未必相同，如果在模型中额外增加一个自变量，即使这个自变量没有经济意义，在统计上也不显著，拟合优度仍可能变大。因此，R2不适合作为衡量拟合优度的尺度。为了避免增加自变量而高估R2，引进了修正自由度的判定系数，其计算公式为：

由于修正自由度的判定系数考虑了样本容量和模型中的参数的个数，这样使得修正的判定系数永远小于原判定系数。

（二）估计标准误差

同一元线性回归一样，多元线性回归中的估计标准误差也是对误差项的方差的一个估计值，它在衡量多元线性回归方程的拟合优度方面也起重要作用。其计算公式：

多元线性回归中对估计标准误差的解释与一元线性回归类似，由于估计标准误差所估计的是预测误差的标准差，其含义是：根据自变量x1，x2，…，xk来预测因变量Y的平均预测误差。

（三）显著性检验

在一元线性回归中，整个方程线性关系的检验（F检验）与回归系数的检验（t检验）是等价的。但是在多元线性回归中，这两个检验不再等价。

1.F检验

F检验主要是检验自变量同多个自变量的线性关系是否显著，在k个自变量中，只要有一个自变量同音变的线性关系显著，F检验就能通过，因此，F检验是对方程整体线性关系的检验。

F检验的具体步骤为：

第一步，提出假设：H0∶b1＝b2＝…＝bk；H1∶b1，b2，…，bk至少有一个不等于0。

第二步，构造F统计量，并在假设条件下计算出F检验统计量。计算公式为：

第三步，做出统计决策。给定显著性水平α，根据分子自由度（k）、分母自由度（n－k－1），查F分布表得Fα。若F＞Fα，则拒绝原假设；若F＜Fα，则接受原假设。

2.t检验

回归系数显著性检验要采用t检验。t检验是对每个回归系数分别进行单独的检验，主要用于检验每个自变量对因变量的影响是否都显著。

t检验的具体步骤为：

（1）建立假设。

H0∶bi＝0；H1∶bi≠0

（i＝1，2，3，…，k）

（2）选择统计量。(www.daowen.com)

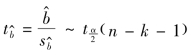，其中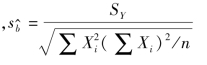

（3）根据给定的显著性水平和自由度，查找t分布表中相应的临界值

（4）计算上述的统计量并与查表的值进行比较，若，则拒绝原假设H0，这样认为，变量间存在线性关系；若，则不能拒绝原假设H0，可以认为变量间的线性关系不存在。

【例6－7】某种商品的价格指数、售后服务指出、替代产品销售量均会影响该产品的销售额，下表是三个影响因素对销售额的影响数据。试分析它们对销售额的影响。

续表

解：经Analyze—Regression—Linear菜单进入回归分析对话框。将Y选为因变量；X1、X2、X3选为自变量。点击OK。主要过程和结果如下。

Variables Entered／Removed（b）

a　All requested variables entered.
b　Dependent Variable：销售额

Model Summary

a　Predictors：（Constant），替代品额，价格指数，售后支出

ANOVA（b）

a　Predictors：（Constant），替代品额，价格指数，售后支出
b　Dependent Variable：销售额

Coefficients（a）

a　Dependent Variable：销售额

根据上述结果，写出多元线性回归方程：

变量X1的回归系数是－7．431，其统计含义是：在其他两个因素不变的情况下，价格指数每增加一个单位，该产品销售额“平均”下降7．431个单位；变量X2的回归系数是1．582，其统计含义是：在其他两个因素不变的情况下，售后服务支出每增加一个单位，该产品销售额“平均”上升1．582个单位；变量X3的回归系数是－0．732，其统计含义是：在其他两个因素不变的情况下，替代产品销售额每增加一个单位，该产品销售额“平均”下降0．732个单位。

回归模型的统计检验：

拟合优度评价：回归模型的修正判定系数是0.925，说明92.5%的产品销售额可以用该产品价格指数、售后服务支出和替代品销售额这三个因素来解释。说明该方程的拟合效果较好。

方程整体的显著性检验。从F统计量的计算值与给定显著性水平的F统计量值为3．55的比较后，可以判断方程的显著性可以通过。

单个参数的显著性检验。从t统计量的计算值与给定显著性水平的t统计量为2．101的比较后，可以判断X1、X2对销售额的影响是显著的；而X3对销售额的影响不能确定。