回归分析的主要任务是建立能够近似反映真实总体回归函数的样本回归函数。在根据样本资料确定样本回归方程时，总是希望y的估计值y＾从总体上能够尽可能地接近其实际观察值，通过前面的分析可知a、b是未知参数，需要根据变量y和x的样本数据对它们进行估计。在此通常采用最小二乘估计。利用最小二乘估法得到的估计值a＾和b＾称为a和b的最小二乘估计，这样可设一元线性回归方程为：y＝a＾＋b＾x。这是一条回归直线，a＾和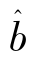为常数，决定了直线的位置。

对于每一个观察值xi利用公式计算得到的回归值与实际值yi并不一定相等，而是存在一定的偏差，这个偏差定义为残差，记作ei。残差可正可负。

最小二乘法（OLS）原理就是使得最小，

设最小值，把代入上式，得

＝最小值

根据微积分求极值的定理，要使上式成立，应分别将对a和b求偏导数并令其等于0，即得

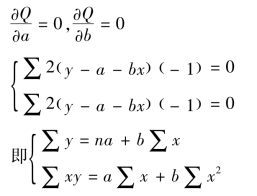
这就是求解参数a，b的二元一次方程组。解之即求得a，b的公式如下：

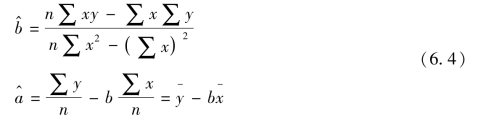
1.使用未分组资料拟合一元线性回归模型举例

【例6－3】以【例6－2】数据为例，试估计回归方程的参数。

解：设估计参数方程为：

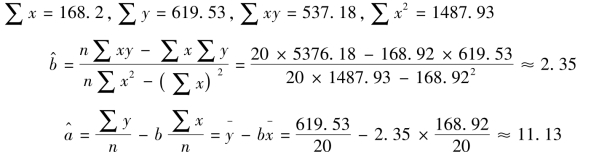
把b和a的值代入回归方程则，

这个回归方程告诉我们：随着广告费用的增加，产品销售额也增加，在不考虑其他因素的情况下，投入广告费用1百万元，产品销售额期望增加的估计值是2．35百万元。(www.daowen.com)

2.使用分组资料拟合一元线性回归模型举例

分组资料拟合一元线性回归模型的方法步骤与未分组资料基本相同，其主要区别在于求待定参数时要注意加权。其标准方程组为：

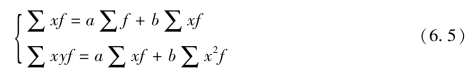
求参数a和b的公式为：

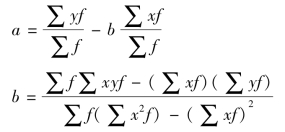
现根据表6－7资料，说明其计算过程。

表6－7　分组资料回归直线模型计算表

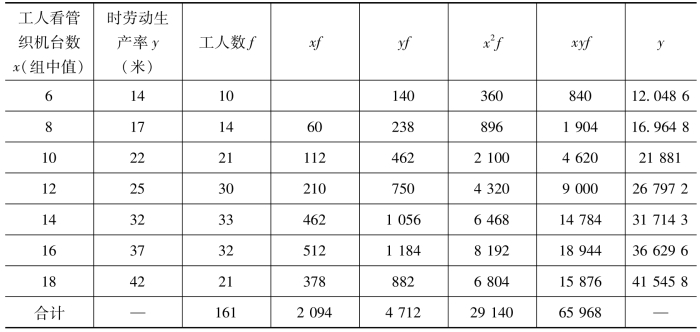
由表6－7资料得出：

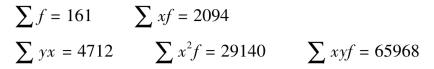
将这些资料代入上述求参数a和b的公式得：

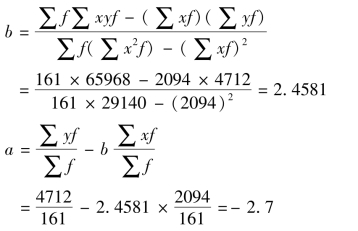
则所求的一元线性回归模型为：

y＝－2．7＋2．4581x