在人们的日常生活中，经常会发现这样的现象：虽然某种事物的变化是众多因素作用的结果，但其中却有一个主要的因素，它往往是我们研究的首要对象。例如，居民可支配收入的增加是其消费支出增加的首要原因。

根据表6－6的数据画出产品销售与广告费用之间的散点图，如图6－3所示。

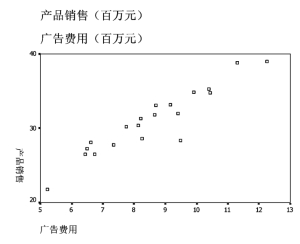
图6－3　产品销售与广告费用的散点图(www.daowen.com)

从图6－3可以看出，样本数据点大致落在一条直线附近，可以判断产品销售与广告费用之间存在线性关系，同时，还可以发现，样本点并不完全落在直线上，也就是说产品销售并不完全由广告费用所确定。实际上，影响产品销售额的因素还有许多，比如，居民收入水平、人口总量等，样本点与直线之间的差异可以看作其他所有因素造成的结果。

如果将上例中的广告费用看作是自变量x，产品销售额作为因变量y，变量x与y之间基本上是线性关系，将除广告费外的其他因素作为随机因素处理。因此，可以假设变量x与y有下列关系：y＝a＋bx＋ε。这就是产品销售额与广告费用的一元线性回归模型。它表明广告费用是决定产品销售额的主要因素。两者之间有密切的关系，但密切的程度又没有达到由x唯一确定y的地步。其中a称为常数项，表示不受广告费用影响的产品销售额；b表示广告费用每增一个单位时，产品销售额所增加的数量；ε表示影响产品销售额变化的其他因素，如居民收入水平、人口总量等。

一般情况下，对于所研究的对象获得n组样本观察值(x1，y)1，(x2，y)2，…，(xn，y)n，如果它们符合y＝a＋bx＋ε，则有yi＝a＋bxi＋εi，这就是一元线性回归模型。式中，y是被解释变量，x是解释变量，ε是随机项，表示其他影响因素，a、b是回归系数。

随机误差项是不可预测的，在实际应用中，为了回归分析的需要，对模型中的随机误差项有以下基本假设：第一，随机误差项εi（i＝1，2，…，n）服从正态分布；第二，随机误差项εi（i＝1，2，…，n）的期望值是0，E（εi）＝0；第三，随机误差项的方差是一个定值，即Var（εi）＝σ2（i＝1，2，…，n）；第四，任意两个随机误差项相互独立，无自相关，即Cov（εi，εj）＝0（i，j＝1，2，…，n，i≠j）；第五，随机误差项与自变量不相关，即Cov（ε，x）＝0。以上基本假设是由著名德国数学家高斯最早提出来的，因此也称为高斯假设，满足以上假设条件的一元线性回归模型称为标准一元线性模型。