（一）r的抽样分布

1.r的抽样分布随总体相关系数和样本容量的大小而变化

当样本数据来自正态总体时，随着n的增大，r的抽样分布趋于正态分布，尤其是在总体相关系ρ数很小或接近0时，趋于正态分布的趋势非常明显。而当远离0时，除非n非常大，否则r的抽样分布呈现一定的偏态。

2.当ρ为较大的正值时，r呈现左偏分布；当ρ为较大的负值时，r呈现右偏分布。只有当ρ接近于0，而样本容量n很大时，才能认为r是接近于正态分布的随机变量。

（二）检验的步骤

1.检验两个变量之间是否存在线性相关关系

2.等价于对回归系数b1的检验

3.采用R.A.Fisher提出的t检验

4.检验的步骤为：

（1）提出假设：H0∶ρ=0；H1∶ρ≠0。

（2）计算检验的统计量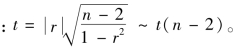

（3）确定显著性水平α，并做出决策。

若|t|＞t2/α，拒绝H0；

若|t|＜t2/α，不拒绝H0。

【例6－2】为研究某类产品广告费用与销售额之间的关系，根据调查取得20个样本数据，如表6－6所示。(www.daowen.com)

表6－6　某产品销售额与广告费用数据情况　单位：百万元

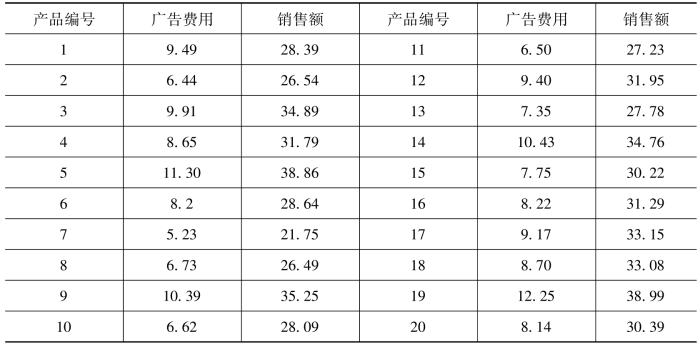
试计算：

（1）产品销售额与广告费用的相关系数。

（2）对上述相关系数进行显著性检验（显著性水平α＝0．05）。

解：根据上表的数据有：

∑x＝168．2，∑y＝619．53，∑xy＝537．18，

∑x2＝1487．93，∑y2＝19546．58

由公式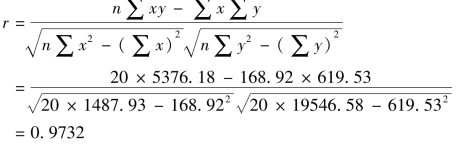

提出假设，H0：ρ＝0；H1：ρ≠0

构造并计算统计量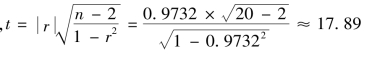

根据显著性水平α＝0．05，查t分布表，得：

由于t≈17．89＞＝2．101，所以拒绝原假设，即相关系数在统计上是显著的。这样认为，产品销售与广告费用之间存在显著的相关关系。