判断现象间的相关关系，一般先作定性分析，然后做定量分析。定性分析就是根据经济理论，有关专业知识和实际工作经验，进行科学的分析研究，初步确定现象间有无相关关系，如确有相关关系，进一步编制相关图和相关表，可以直接地判断现象之间大致上呈现何种关系形式，以此计算相关系数做定量分析，精确反映相关关系的方向和程度。

（一）编制相关表

由总体单位的原始资料还可以编制相关表。根据资料是否分组，相关表有简单相关表和分组相关表两种。

1.简单相关表

简单相关表是一种反映变量之间相关关系的统计表，将某一变量按其取值的大小排列，然后再将与其相关的另一变量的对应值平行排列，便可得到简单的相关表。如表6－1所示。

表6－1　产品产量和生产费用相关表

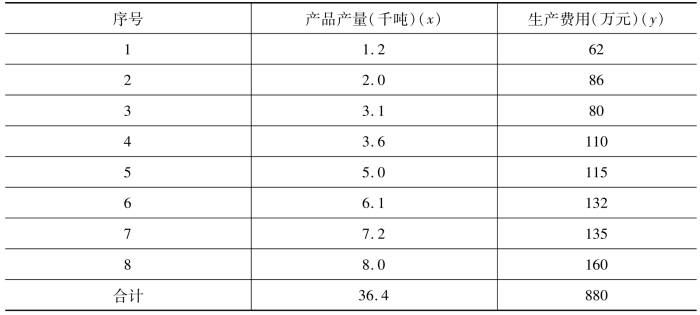
从表6－1中可以看出，产品生产量和生产费用之间关系虽不十分严格，但有直线相关的趋势，而且大致可以看出关系比较密切。

2.分组相关表

如果原始资料很多，运用简单相关表来表示就很难使用了。为了排除偶然因素的影响和使资料表达更简明，就要将原始资料进行分组，然后编制相关表，这种相关表称为分组相关表。分组相关表包括单变量分组表和双变量分组表两种。

（1）单变量分组表。单变量分组相关表是依据自变量进行分组，并列出每组变量值出现的次数和因变量值的统计表。如表6－2所示。

表6－2　单变量分组相关表

从表6－2中可以看出，平均亩产量随耕作深度的增加有增加的趋势。

（2）双变量分组表。对两种有关变量都进行分组，交叉排列，并列出iangzh变量各组间的共同次数，这种统计表称为双变量分组相关表。例如，根据某汽运公司的汽车运木材成本和运量的资料，编制双变量分组相关表，如表6－3所示。

表6－3　双变量分组相关表

制作双变量分组相关表，应注意将自变量放在横栏，按变量值从小到大、自左至右排列，将因变量放在纵栏，按变量值从大到小、自上而下排列，所以做这种安排，是为了使相关表与相关图一致起来，能直观地看出变量之间的相关情况。

从表6－3中可以看出，当木材运量较小时，相应运木材成本较高；当木材运量较大时，运木材成本较低。由此说明，在一定条件下，运量越大，运输成本越低；反之，运量越小，运输成本越高。

如果与某个现象相关的因素不止一个，可以分别绘制出许多相关图，从许多相关图的对比中，大致可以看出与各因素关系的大小，从中判断出哪个是主要因素，哪个是次要因素。

（二）绘制散点图

散点图也叫相关图或散布图，是以直角坐标系的横轴代表变量x，纵轴代表变量y，将两变量相对应的成对数据用坐标点的形式描绘出来，用于反映两变量之间相关关系的图形。

例如，研究结果表明，受教育时间与个人的薪金之间呈正相关关系。研究人员搜集了不同行业在职人员的有关受教育年数和年薪的数据如下：

表6－4　受教育年数与年薪一览表

由表6－4的资料绘制的相关图如图6－2所示。

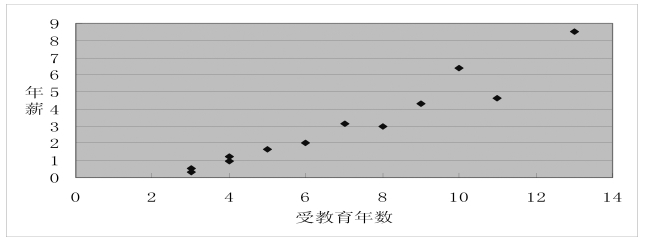
图6－2　受教育年数与年薪的散点图

（三）相关系数的计算与应用

相关图、相关表可以帮助人们直观地看出所研究的变量之间是否存在相关关系，以及所呈现出的相关关系形式，但是不能确切地表明相关关系的密切程度。当两个变量存在直线相关时，一般借助相关系数这一指标说明其相关的密切程度。

什么是相关系数？它是研究和判断两个变量之间直线相关关系密切程度和方向的统计指标，一般用r表示。

相关系数比相关图更能概括表现相关的形式和程度。根据相关系数的大小，或把若干相关系数加以对比，可以发现现象发展中具有决定意义的因素，因而相关系数对于判断变量之间相关关系的密切程度，具有重要的作用。

相关系数具有以下几个特点和性质。

1.相关系数的大小只能判断两个变量之间是否有直线相关关系及其密切程度和方向，而不能作为曲线相关关系的判断依据。比如，当相关关系很小甚至为零时，只能说明变量之间不存在直线相关而不能说它们不存在相关关系。曲线相关关系的密切程度判断方法是计算相关指数指标。

2.测定相关关系时是无需分辨自变量和因变量的，所以两个变量之间如果存在直线相关关系，则计算的相关系数只有一个。

3.相关系数的计算，要求两个变量的数据都是随机抽选的，即在选择计算相关系数所需统计资料时，所有数据不能凭选用者主观愿望来确定，这样才能保证计算结果的客观、准确。

4.相关系数有正负之分。当相关系数为正值时，说明两个变量之间存在着正相关关系；反之，相关系数为负值时，说明两个变量之间存在着负相关关系。(www.daowen.com)

5.相关系数取值范围为愈接近1，说明两个变量之间的直线相关关系密切程度就愈高；｜r｜愈接近0，则直线相关关系的密切程度就愈低，在实际应用中，利用相关系数判断直线相关关系的密切程度的一般标准是：

当时，说明两个变量之间不存在直线相关关系。

当时，认为两个变量微弱直线相关。

当时，认为两个变量低度直线相关。

当时，认为两个变量显著直线相关。

当时，认为两个变量高度直线相关。

当时，说明两个变量之间存在完全直线相关关系即成直线函数关系。

根据相关表的资料，相关系数（r）的计算方法：

1．积差法

r表示相关系数

表示自变量数列和因变量数列的协方差

σx表示自变量数列的标准差

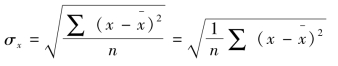
σy表示自变量数列的标准差

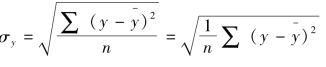
所以相关系数也可写成：

【例6－1】研究结果表明，受教育时间与个人的薪金之间呈正相关关系。研究人员搜集了不同行业在职人员的有关受教育年数和年薪的数据，见表6－5所示。

表6－5　相关系数计算表

续表

试计算受教育时间与个人的薪金之间的相关系数。

解：

根据相关系数可知，受教育时间与个人的薪金之间呈现高度正相关关系。

2．相关系数简捷计算方法

积差法相关系数在计算过程中要使用两个数列的平均值计算比较烦琐。相关系数的基本计算公式，还可以利用代数推算的方法形成许多简捷公式：

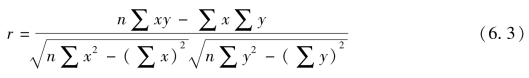
根据上述例6－1计算：

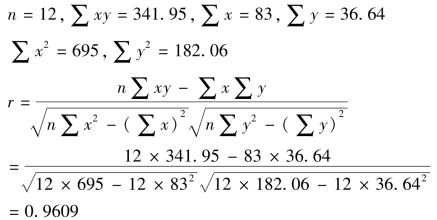
在已有平均值及标准差的情况下也可以使用以下公式：

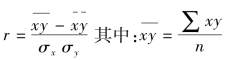
所有这些计算方法，其实只是积差法相关系数的变形。了解了公式中各项指标的关系，可以根据已有的材料选用适当的方法。