这里仅介绍一个正态总体参数的假设检验。

在对总体均值进行假设检验时，要考虑总体是否服从正态分布，总体方差是否已知以及样本容量的大小，以便确定检验统计量。一个正态总体参数的假设检验可分为以下几种情况：

（一）总体方差已知的均值检验

某食品企业要对其出厂的奶粉进行重量检验，每瓶的标签上标明其重量是500克。以双侧检验为例，在总体服从正态分布，总体方差σ2已知，对总体均值μ进行假设检验的一般步骤：

1.确定原假设和备择假设

首先假定该厂产品的重量是合格的。如果奶粉总体中每瓶的平均重量为500克，那么其产品是合格的；如果奶粉总体中每瓶的平均重量远远大于或者小于500克，那么其产品的重量是不合格的。得到如下形式的原假设和备择假设：

H0：μ＝500

H1：μ≠500

如果样本数据表明不能拒绝H0，则统计证据不支持做出认为该批奶粉不合格的结论，但是如果样本数据表明能拒绝H0，则可以得出备择假设为真的结论，在这种情况下，可以做出产品重量不足的结论。

2.选取检验统计量

假定选取100瓶奶粉组成一个随机样本。如果这100瓶奶粉的重量的样本均值不等于500克，则样本结果对原假设H0：μ＝500质疑。那么，当样本均值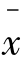比500克多多少或少多少的时候，才能冒着犯第二类错误的危险拒绝该批产品是合格的呢？

假定最初的原假设H0：μ＝500是真的。由中心极限定理知道，只要是大样本容量（n≥30），则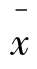的抽样分布就近似地服从正态分布，即样本均值

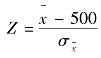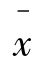的值说明了与μ＝500之间相差多少个标准差。对于总体均值的假设检验，以Z作为检验统计量来确定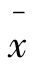与μ＝500之间的距离是否足够远，进而判断是否拒绝原假设。Z＝±1说明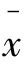在μ＝500上下侧各0．5个标准差（正态分布是对称的）；Z＝±2说明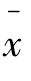在μ＝500上下侧各一个标准差，以此类推。当原假设为真时，Z的值小于－3几乎是不可能发生的。问题关键是：当检验统计量的Z值为多少时，才有足够的证据来拒绝原假设。

3.选定显著性水平α，查表求临界值

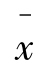在μ＝500为中心上下两侧1．645个标准差的概率为0．05。因此，当检验统计量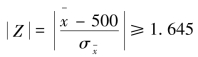时，如果拒绝原假设，则发生第一类错误的概率为0．05。如果该厂将水平0．05作为可以接受的第一类错误的概率，则当检验统计量表明样本均值在μ＝500上下两侧1．645个标准差时，将拒绝原假设。于是，当时，将拒绝H0。

在假设检验的方法中，要求事先指定第一类错误的最大允许概率值，并称这一最大概率值为该检验的显著性水平，以α表示，代表当原假设为真时，发生第一类错误的概率。管理者必须事先制订这一显著性水平。如果发生第一类错误的成本很高，则可以适当选择较大的值为显著性水平。

4.计算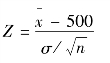

假定该厂的负责人选择第一类错误的最大概率为0．05。因此，该假设检验中显著性水平α＝0．05。当原假设μ＝500为真时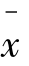，在均值500上下两侧并与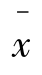距离大于1．96个标准差的概率为0．05。因此，可以建立如下拒绝规则。

如果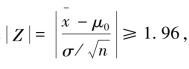则拒绝H0；

如果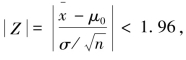则接受H0。

5.做出决策

若拒绝H0；

若接受H0。

【例5－14】根据过去大量资料，某厂生产的灯泡的使用寿命服从正态分布，均值为1050个小时，标准差为100小时。现从最近生产的一批产品中随机抽取25只，测得样本平均寿命为1100小时。试在0．05的显著性水平下判断这批产品的使用寿命是否有显著变化。（α＝0．05）

解：依题意知是属于双侧检验

建立原假设和备择假设：

H0：μ＝1050

H1：μ≠1050

构造检验统计量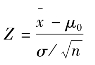

由样本观测值，得

由α＝0．05，查表得

由于，所以拒绝原假设H0，认为该批产品的使用有显著变化。

若是单侧问题，在同样的小概率标准下，除临界值有变化外，其他步骤与双侧检验相同。其检验规则为：

当假设：(www.daowen.com)

H0∶μ≤μ0

H1∶μ＞μ0

若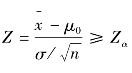时，拒绝H0；

若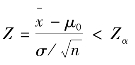时，接受H0。

当假设：

H0：μ≥μ0

H1：μ＜μ0

若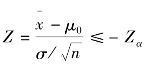时，拒绝H0；

若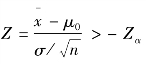时，接受H0。

（二）总体方差未知的均值检验

当总体服从正态分布，但是总体方差σ2未知时，则要用总体方差的无偏估计量——样本方差s2来代替σ2，检验统计量及其分布为：

利用服从t分布的统计量去检验总体均值的方法称t检验法。具体的步骤同方差已知的情况一样。下面举例来说明。

【例5－15】一个汽车轮胎制造商声称，某一等级的轮胎的平均寿命在一定的汽车重量和正常行驶条件下大于40000公里，对一个由25个轮胎组成的随机样本做了试验，测得平均值为41000公里，标准差为5000公里。已知轮胎寿命的公里数服从正态分布，我们能否根据这些数据做出结论，该制造商的产品同他所说的标准相符？（α＝0．05）

解：按题意需检验

H0∶μ≥40000

H1∶μ＜40000

取α＝0．05，由表可知，此检验问题的拒绝域为：

又已知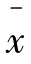＝41000，s＝5000，即有：

t没有落在拒绝域内，因此接受H0，即有证据表明轮胎使用寿命显著地大于40000公里。

（三）总体比例的假设检验

总体比例的假设检验是检验总体单位中含有某种特征的单位数占的比例是否为某一假设值p0，由中心极限定理可知，服从二项分布的样本比例在大样本的情况下近似服从正态分布。对总体比例的检验通常是在大样本的条件下进行的，采用Z检验法进行检验。总体比例的假设检验问题也考虑了以下三种类型：

（1）H0：μ≤μ0；H1：μ＞μ0；

（2）H0：μ≥μ0；H1：μ＜μ0；

（3）H0：μ＝μ0；H1：μ≠μ0。

选择检验统计量为：

【例5－16】某研究者估计本市居民家庭的电脑拥有率为85%。现随机抽查了200个家庭，其中168个家庭拥有电脑。试问研究者的估计是否可信？（α＝0．05）

解：这是一个总体比例的假设检验问题。根据题意：

设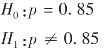

确定检验统计量：

对给定的显著性水平α＝0．05，查表得

计算Z值：Z＝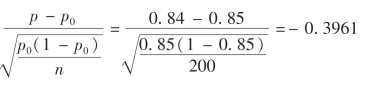

所以接受H0，由此判断研究者的估计可信。