（一）点估计

点估计，又称定值估计，就是用实际样本指标数值作为总体参数的估计值。点估计的方法简单，一般不考虑抽样误差和可靠程度，它适用于对推断准确程度与可靠程度要求不高的情况。

例如表示以样本算术平均数作为总体算术平均数X－的估计量，并根据实际抽样调查资料计算样本平均值作为总体平均数参数的估计值。例如，根据某地区样本资料计算粮食亩产650公斤，就以这个数字作为全地区粮食亩产水平的估计值。

在统计中经常使用的点估计量有：

上式中，大写字母的分别是总体的均值、成数与方差分别表示相应的估计量；小写字母的与分别是样本均值、样本成数与样本方差。

【例5－8】对某企业的产品进行抽样检验，设抽出200件产品，其中不合格产品10件，试问该企业产品的合格率是多少？

我们可以通过样本的合格率来估计企业产品的合格率。样本的合格率p＝190／200＝95%，我们估计该企业产品的合格率为95%。

点估计的优点是直接给出了总体参数的估计值，通过样本资料就能得到总体参数的具体数据。不足之处是不能提供估计误差的信息。因此，我们有必要考虑点估计的优良性。由于抽样的随机性，样本统计量是一个随机变量。因此，从一次抽样的结果来判断一个统计量的优良性是不确切的，必须通过多次试验才能判断这个估计量是否在某种意义上接近被估计的总体参数的真值。这里提到的“某种意义”，具体来说就是点估计优良性的三条标准：无偏性、有效性和一致性。

估计总体参数，未必只能用一个统计量，也可以用其他统计量。例如估计总体平均数，可以用样本平均数，也可以用样本中位数、众数，等等。应当以哪一种统计量作为总体参数估计量才是最优的，这就有评价统计量的优良估计标准问题。作为优良的估计量应该符合以下三个标准：

（1）无偏性。无偏性即样本统计量的期望值（平均数）等于被估计的总体参数。

用θ表示总体的待估计参数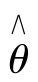，是估计θ的样本统计量，我们说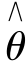是θ的无偏估计，指的是θ满足：

无偏性要求用来估计总体参数的样本统计量，其分布是以总体参数真值为中心的，在一次具体的和抽样估计中，统计量（或估计量）或者大于总体参数，或者小于总体参数；但是，在进行重复抽样估计的过程中，所有样本统计量的平均数应该等于待估计总体参数。这说明，无偏估计要求估计量没有系统偏差。由于，所以样本平均是总体平均的一个无偏估计。

（2）一致性。一致性是指随着样本容量不断增大，样本统计量接近总体参数的可能性就越来越大，或者，对于任意给定的偏差控制水平，两者间偏差高于此控制水平的可能性越来越小，接近于0。用公式表示就是：

（3）有效性。有效性即作为优良估计量的方差应该比其他估计量的方差小。

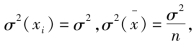如果和都是总体参数θ的无偏估计量，如果，则说明估计量比更有效。设总体的方差是σ2，我们有显然，样本平均数的方差比样本中某个单位的标志值的方差要小，只是方差的1／n，所以样本平均数作为估计量，更加有效。

（二）区间估计

点估计给出总体参数的具体数值，但这个估计值误差有多大？可靠性如何？这些问题点估计都不能回答。区间估计则弥补了点估计这方面的不足。

区间估计就是根据样本指标、抽样误差和概率保证程度去推断总体参数的可能范围。在统计实践中，通常用一个区间及其出现的概率来估计总体参数，并以一定的概率保证总体参数包含在估计区间内，这就是参数的区间估计问题。区间估计是抽样估计的主要方法。进行区间估计要完成两个方面的估计：其一，根据样本指标和抽样平均误差估计总体指标的可能范围；其二，估计推断总体指标真实值在这个范围的可靠程度。

设和都是两个统计量分别作为总体参数θ区间估计的上限与下限，则要求：

式中α（0＜α＜1）是区间估计的显著性水平，其取值大小由实际问题确定，经常取1%、5%和10%；1－α称为置信度。区间估计的特点是：给出总体参数的一个估计区间，总体参数恰好在这个区间内的概率不要求达到1，可放低要求，减去一个小概率的显著性水平，达到1－α就行了。

由于θ作为总体参数，是固定不变的常数，它或者在给出的区间内，或者在给出的区间外，上式的概率或者是0或者是1，不可能是1－α。怎么来理解这个概率？由于和都是统计量表示用区间去框θ，虽然每次结果只能是此区间或者框住了θ，或者没有框住θ，估计结论或者正确或者错误，但是如果多次重复估计的话，则平均100次估计中，只有100α次估计是错误的，有100（1－α）次估计是正确的。

1.平均数的区间估计

对平均数的区间估计，分两种情况：

（1）总体方差σ2已知时：由抽样分布定理知道，如果总体服从正态分布，则样本平均数如果总体正态性不成立，但是样本容量n充分大时，近似的也有¯x～因此，

这样，对于给出的显著性水平α，通过（反）查标准正态分布表可得到临界值zα／2，满足：

P（－zα／2≤z≤zα／2）＝1－α

注意到：

因此：

这就是说，总体平均数在显著性水平α时的区间估计：

反过来，如果平均数抽样的极限误差是即：

等价于一个区间估计这个区间估计的置信度是多少呢？

通过临界值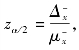去查标准正态分布，可得出上式的置信度是1－α。临界值zα／2与置信度1－α，两者间是密切相关的，通过查标准正态表，可互相确定。如果置信度提高，区间估计的概率增大，α就要相应地减小，临界值zα／2增大；反之，区间估计的概率减小，临界值也减。因此，也称临界值zα／2为概率度，简记为z，用来间接衡量区间估计的概率大小。

关于极限误差、抽样平均误差、概率度三者的关系，有如下结果：

或者：

Δx

－＝zμ

以上式中的μ是抽样平均误差。注意：以上关系式不仅在对平均数进行区间估计时有效，在对成数指标等其他参数估计时也适用，因此式中抽样平均误差省去了下标x－，使公式应用更加广泛（下同）。

对于给出的置信度水平1－α，得到置信区间的公式：

重复抽样：

不重复抽样：

【例5－9】某地区的电视台委托调查公司估计地区内居民平均每日看电视的时间。调查公司随机抽取了100名进行调查，样本数据显示平均每人每天看电视时间是4小时。如果已知总体的标准差σ＝1．5小时。试求：

（1）该地区内居民每天看电视的平均时间的置信区间（置信度是95%）；(www.daowen.com)

（2）如果要求估计的误差不超过18分钟，这时置信度是多少？

解：（1）已知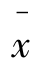＝4小时，n＝100，σ＝1．5小时，1－α＝95%，α＝5%。这时查标准正态分布表，可得临界值：

zα／2＝z0．025＝1．96

由于样本容量在地区居民人数中所占的比重太小，重复与不重复抽样效果相差不大，按重复抽样计算，区间估计是：

因此，可以95%的置信度，估计该地区内居民每天看电视的平均时间在3．70到4．30个小时之间。

要求极限误差等于18分钟，即小时。这时概率度：

查概率表可知这时的概率是95．45%，区间估计是：

因此结论是：可用95．45%的概率保证，估计该地区内居民每天看电视的平均时间在3．70到4．30个小时之间。

（2）总体方差σ2未知时：

当总体服从正态分布但方差未知时，可用样本的标准差s代替总体标准差。这时统计量是：

t服从的分布不是标准正态分布，而是自由度为（n－1）的t分布。因此，总体均值的区间估计是：

重复抽样：

不重复抽样：

以上区间估计公式中，不仅总体标准差σ用样本标准差s代替，而且临界值tα／2（n－1），要查t分布表（自由度为n－1）得到。但是，在大样本场合，t分布与标准正态分布非常接近，可直接从标准正态分布表中查临界值（这时还不受总体正态性的限制）。

【例5－10】设钢珠的直径服从正态分布，现从一批钢珠中随机抽出9个，测量它们的直径，并求得其样本的平均值是31．06毫米，样本标准差是0．25毫米。试以95%的概率保证，估计钢珠直径的置信区间。

解：据题意有：

n＝9，α＝5%，自由度是n－1＝8，查t分布表得到临界值tα／2（n－1）＝t0．025（8）＝2．306

所以钢珠直径的估计区间是：

即以95%的概率保证，这一批钢珠的直径在30．87毫米与31．25毫米之间。

【例5－11】灯具厂质量控制部经理希望估计一批灯泡的平均寿命。现随机地抽取50只灯泡进行测试，其平均寿命是1 600小时，样本方差是2 500小时平方。试给出这批灯泡平均寿命95%的置信区间估计。

解：已知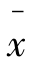＝1600小时，n＝50，s2＝2500（小时）2，s＝50小时，1－α＝95%，α＝5%

由于n大于30，是大样本场合，这时临界值可查标准正态分布表得到：

zα／2＝z0．025＝1．96

因此，区间估计是：

即以95%的置信度，估计该批灯泡的平均寿命在1586．14到1613．86个小时之间。

2.成数指标的区间估计

成数指标是一个特殊的平均数。我们设总体成数是P，样本成数是p，则当样本容量充分大时，则p近似服从，因此，z＝近似服从标准正态分布。

所以，类似于总体平均数的区间估计，总体成数的区间估计是：

p±zα／2μp

式中的成数抽样平均去查在重复抽样条件下是：

在不重复抽样条件下是：

因此，成数抽样平均的区间估计，对于给出的置信度水平1－α，得到置信区间的公式：

在重复抽样条件下是：

在不重复抽样条件下是：

由于总体成数未知，抽样平均误差公式中的总成数用样本成数代替。

【例5－12】某工厂要估计一批总数5000件的产品的废品率，于是随机抽出400件产品进行检测，发现有32件废品。试给出该批产品的废品率的区间估计（置信度是90%）。

解：n＝400，N＝5000，样本废品率，p＝32／400＝8%，置信度1－α＝90%，α＝10%，α／2＝5%。查标准正态分布表得：

zα／2＝z0．05＝1．645

因此，这批产品废品率的区间估计是：

即这批产品的废品率在5．9%与10．1%之间。