下面将简单介绍几种常见的抽样调查组织形式：简单随机抽样、分层抽样、等距抽样、整群抽样。

（一）简单随机抽样

简单随机抽样（也叫纯随机抽样），就是从总体中不加任何分组、划类、排队等，完全随机地抽取调查单位。其特点是每个样本单位被抽中的概率相等，样本的每个单位完全独立，彼此间无一定的关联性和排斥性。简单随机抽样是其他各种抽样形式的基础。通常只是在总体单位之间差异程度较小和数目较少时，才采用这种方法。

采用这种方法时，可用编号抽签的方法，给全及总体各个单位编号，并做成号签，把号签掺和起来，形成明确的抽样框。所谓抽样框就是可以选择作为样本的许多单位或个体所组成的总体。从中任意抽取所需要的单位数，然后按照抽中的号码，对调查单位进行登记。前面各节讨论的抽样方法都是简单随机抽样。

简单随机抽样的误差计算情况如下：

在重复抽样下，样本平均数的抽样极限误差公式为：

在不重复抽样下，样本平均数的抽样极限误差公式为：

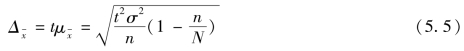
从上式可以看出，必要的样本单位数受允许的极限误差的制约，极限误差要求愈小则样本单位数就要愈多。所以在抽样组织中对抽样误差可能允许的范围要十分慎重地考虑。

对一个总体进行多指标抽样调查时，所要求的样本单位数可能不同，应该采用其中较多的单位数，以保证两个指标的误差不超过预定的要求。

简单随机抽样在理论上是最符合随机原则的，它的抽样误差容易得到理论上的论证，因此可以作为发展其他抽样组织形式的基础，同时也是衡量其他抽样方式抽样效果的比较标准。

但是，简单随机抽样在实践中受到许多限制，例如当总体很大时，对每个单位加以编号就有很大的困难。特别是有些现象根本无法进行简单随机抽样，如对正在连续不断地大量生产的工业产品进行质量抽查时，就不可能采用简单随机抽样的方式。

（二）分层抽样

分层抽样就是将总体单位按其属性特征分成若干类型或层，然后在类型或层中随机抽取样本单位。其特点是：由于通过划类分层，增大了各类型中单位间的共同性，容易抽出具有代表性的调查样本。该方法适用于总体情况复杂，各单位之间差异较大，单位较多的情况。

类型抽样误差计算和简单随机抽样误差的计算方法只有一个区别，就是用平均组内方差代替总体方差。

推断平均数的误差公式为：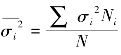

式中表示平均组内方差。

推断成数的误差公式为：

式中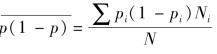表示成数的平均组内方差。

【例5－4】从250家超市中抽取50家进行一季度销售额的调查。具体数据资料见表5－5所示。

表5－5　50家超市一季度销售额资料

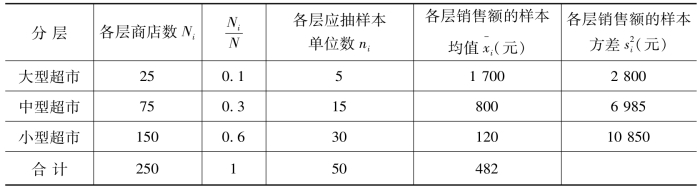
试求样本平均销售额和抽样平均误差。

解：所有样本均值为

(www.daowen.com)

重复抽样：μx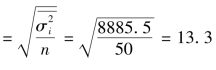

不重复抽样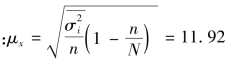

类型抽样的抽样平均误差只取决于组内方差的平均水平，不受组间方差的影响。它小于简单随机抽样的抽样平均误差，因此在对总体进行分组时，应尽量扩大组间方差，缩小组内方差。（总方差＝组内方差＋组间方差）

类型抽样是一个比较理想的抽样组织方式。由于进行了分类，影响抽样误差的只是各个组内的方差，而各个组内的方差是比较小的，抽样误差也比较小。所以类型抽样一般较简单随机抽样更为精确。特别是当总体单位标志值大小悬殊时，由于划分类型，保证样本在各种类型中都有比较均匀地分布，故类型抽样较之简单随机抽样可以获得更为可靠的结果。

（三）等距抽样

等距抽样是将总体各单位按一定标志或次序排列成为图形或一览表式（也就是通常所说的排队），然后按相等的距离或间隔抽取样本单位。其特点是：抽出的单位在总体中是均匀分布的，且抽取的样本可少于纯随机抽样。等距抽样既可以用同调查项目相关的标志排队，也可以用同调查项目无关的标志排队。等距抽样是实际工作中应用较多的方法，目前我国城乡居民收支等调查，都是采用这种方式。

1.无关标志排队法

在将总体单位进行排队的时候，采用与调查项目没有关系的标志排队。这是实际工作中常用的一种方法。如产品质量检验，即每隔一定的时间间隔或产量间隔抽取一件产品进行检验，一直抽到预定的样本单位数为止。

无关标志等距抽样的排队顺序的标志与人们研究的目的没有关系，那么它的抽样误差十分接近简单随机抽样的误差。为简单起见，可以采用简单随机抽样误差公式来近似地反映。即：

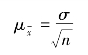
或

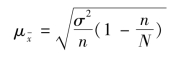
2.有关标志排队法

按照与调查项目的数量有关系的标志排队，即把全及总体按有关标志排队，然后按相等的间距进行抽选样本。这种方法可以看作一种情况特殊的分类抽样。不同的是分类更细致，组数更多，而在每个组内只抽选一个样本单位。因此，一般认为可以用类型抽样的误差公式来计算抽样误差。即：

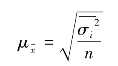
或

（四）整群抽样

整群抽样是从总体中成群成组地抽取调查单位，而不是一个一个地抽取调查样本。其特点是：调查单位比较集中，调查工作的组织和进行比较方便。但调查单位在总体中的分布不均匀，准确性要差些。因此，在群间差异性不大或者不适宜单个地抽选调查样本的情况下，可采用这种方式。例如要抽查学校四级考试通过的情况，不是直接抽学生，而是以班为单位，抽选若干班，然后对这些班的全体学生进行调查。

整群抽样一般都是按不重复抽样方法进行的，所以抽样平均误差为：

上式中：

R表示全及总体总划分的群数；r表示被抽选的群数；σ2表示组间方差。

【例5－5】某工厂大量连续生产，为了掌握某月份某种产品的一级品率，确定抽出5%的产品，即在全月连续生产的720小时中，按每隔20小时抽取1小时的全部产品进行检查。根据抽样资料计算结果，一级品率为85%，各群间的方差为6%，则整群抽样的误差计算如下：

R＝720小时，r＝720×5%＝36小时，为了保证所抽取的36个小时能在720小时中均匀分配，故每隔20个小时（720÷36＝20）抽取1小时，则：

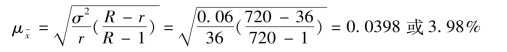
整群抽样和其他抽样方式比较，组织工作比较方便，节省经费开支。但是在抽样单位数目相同的条件下，抽样误差较大，代表程度较低，因为抽选单位比较集中，极大地影响了全及总体各单位分布的均匀性。所以在统计实践中，采用整群抽样时，一般都要比其他抽样方式抽选更多的单位，以便降低抽样误差，提高抽样结果的准确程度。