（一）抽样平均误差的概念

抽样平均误差是指所有可能出现的样本指标的标准差，也可以说是所有可能出现的样本指标和总体指标的平均离差。抽样实际误差是指样本指标值与被推断的总体指标值之差。抽样实际误差是无法知道的，而抽样平均误差是可以计算的。在讨论误差时指的是抽样平均误差。

（二）抽样平均误差的计算

从理论上讲，抽样平均误差是反映抽样误差一般水平的指标。

抽样误差是样本平均数（或成数）与全及总体平均数（或成数）之间的平均离差。用标准差表示：

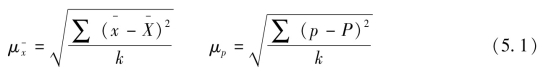
式中，k代表全部可能的样本数目。

抽样平均数（或成数）通过抽样调查可以得到，而全及平均数（或成数）往往是不可能得到的未知数。所以，实际上无法得到抽样平均误差。用数理统计方法推理计算，可以得到抽样平均误差代替理论上的抽样误差。它是依据多次抽样取得的抽样平均数（或成数）所接近的正态分布的原理计算出来的标准差，以说明抽样平均数（或成数）与全及平均数（或成数）之间的平均离差。这个说明平均离差的标准差的指标就是抽样平均数（或成数）的平均误差指标，即抽样平均误差。计算公式如表5－1所示。

表5－1　抽样平均误差公式

表中，ux－表示平均数的抽样平均误差；up表示成数的抽样平均误差；σ2表示全及总体方差；p（1－p）表示成数方差。

从以上计算公式看出，不重复抽样比重复抽样多一个附加因式可近似写成1－这是个永远小于1的正数。若全及总体数目相当大，而抽样总体相当小时，附加因式接近于1，这时，有放回抽样与无放回抽样两个公式计算结果极其接近。但是，无放回抽样平均误差总小于有放回抽样误差。所以，在实际工作中常采用无放回抽样方式，而在计算抽样平均误差时往往采用有放回抽样公式。

计算抽样误差时要使用总体方差σ2或总体标准差σ的资料，而这个资料往往是没有的，为此有以下几种解决方法。

（1）用估计的资料。例如，在农作物产量抽样调查中用农作物预计产量的资料计算出总体方差。

（2）用过去调查所得的资料。可以用全面调查的资料，也可以用抽样调查的资料。如果有几个不同的总体方差的资料，则应该用数值较大的。

（3）用样本方差代替总体方差。概率论的研究从理论上做了证明，样本方差可以相当接近于总体方差，这是实际工作中经常使用的一种方法，但它只能在调查之后才能计算。

如果没有过去的资料，又需要在调查之前就估计出抽样误差，可以在大规模调查之前，组织一次小规模的实验性调查。

从表5－1的公式可以看出：在计算有放回抽样的平均误差时：

①抽样平均数的标准差即抽样平均误差比总体标准差小得多，仅为总体标准差的(www.daowen.com)

②可以通过调整样本单位数n来控制抽样平均误差。若将样本单位数扩大为原来的4倍，则平均误差缩小一半，而抽样平均误差允许扩大一倍，则样本单位数只需要原来的1／4。

【例5－1】假设某电子产品在3000耐用小时以下为不合格品，现在用简单随机抽样方法，从某日生产的2000个产品中抽取5%对其耐用时数进行检验。其结果如下表5－2所示：

表5－2　100个样本电子产品的耐用数资料

根据以上资料，要求：

（1）按放回抽样与无放回抽样计算该产品平均寿命的抽样平均误差。

（2）按放回抽样与无放回抽样计算该产品合格率的抽样平均误差。

解：根据资料可算出：

表5－3　抽样平均误差计算表

（1）有放回抽样下平均寿命抽样平均误差：

无放回抽样下平均寿命抽样平均误差：

（2）有放回抽样下合格率抽样平均误差：

无放回抽样下合格率抽样平均误差：