（一）全及总体和样本

全及总体是研究对象，而样本总体则是观察对象，两者是有区别而又有联系的不同范畴。

全及总体又称母体，简称总体，它是指所要认识的，具有某种共同性质的许多单位的集合体。总体的单位数通常都是很大的，甚至是无限的，这样才有必要组织抽样调查，组成总体的总体单位数用N表示。

如果总体的单位数是有限的，则称该总体为有限总体；如果总体的单位数是无限的，则称该总体为无限总体。

样本总体又称子样，简称样本，是从全及总体中随机抽取出来，代表全及总体的那部分单位的集合体。样本总体的单位数称为样本容量，通常用小写英文字母n来表示。随着样本容量的增大，样本对总体的代表性越来越高，并且当样本单位数足够多时，样本平均数愈接近总体平均数。统计上把样本单位数与全及总体单位数之比称为抽样比例，即

样本按照样本单位数多少分为大样本和小样本。一般讲，样本单位数达到或超过30个称为大样本，否则称为小样本。社会经济现象的抽样调查多取大样本，自然实验观测则多取小样本。

如果说对于一次抽样调查，全及总体是唯一确定的，那么样本总体就不是这样，样本是不确定的，一个全及总体可能抽出很多个样本总体，样本的个数与样本的容量有关，也和抽样的方法有关。

（二）总体参数和统计量

1.总体参数

总体参数又称为全及指标，是根据全及总体各个单位的标志值或标志属性计算的，用来反映总体某种属性或特征的综合指标。常用的全及指标有总体平均数（或总体成数）、总体标准差（或总体方差）。

（1）总体平均数。对于变量总体，它是总体各单位数量标志值的平均数，通常用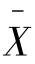表示。

设X为总体的某一变量，其N个变量值为X1，X2，…，XN，则总体平均数为：

在总体未分组的情况下：(www.daowen.com)

在总体分组的情况下：

（2）总体成数。对于属性总体，由于各单位标志不能用数量表示，因此总体参数通常以成数或比重来表示。通常以P表示总体中具有某种标志表现即“是”的单位数在总体单位数中所占的比重，以Q表示不具有某种标志表现即“非”的单位数所占的比重。

设总体N个单位中，有N1个单位具有某种标志表现，N0个单位不具有某种标志表现，且N＝N1＋N0，则总体成数为：

（3）总体方差和标准差。根据总体各单位标志值计算的方差称为总体方差，用符号σ2表示；σ为总体标准差。总体方差的计算公式为：

在总体未分组的情况下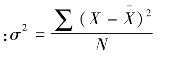

在总体分组的情况下

（4）总体成数的方差和标准差：方差＝P（1－P）；标准差

2.统计量

样本统计量又称样本指标，由样本总体各单位标志值计算出来反映样本特征，用来估计全及指标的综合指标（抽样指标）。统计量是样本变量的函数，用来估计总体参数，因此与总体参数相对应，统计量有样本平均数（或抽样成数）、样本标准差（或样本方差）。

对于一个问题全及总体是唯一确定的，所以全及指标也是唯一确定的，全及指标也称为参数，它是待估计的数。而统计量则是随机变量，它的取值随样本的不同而发生变化。