有些社会经济现象在某些方面的特征，只表现为两种性质上的差异，即标志取值仅有两种可能，非此即彼。例如，产品的质量表现为合格或不合格；对某一电视节目，观众表现为收看或不收看；打靶结果有打中或未打中，等等。这些只表现是或否、有或无、对或错的标志称为是非标志，也称作交替标志。在进行抽样估计时，是非标志的标准差或方差有着重要意义。

（一）成数

是非标志只有两种表现，我们把具有某种表现或不具有某种表现的单位数占总体单位数的比重称为成数。

【例4－29】一批产品共1000件，合格的970件，不合格的30件。合格产品占全部产品的97%，不合格产品占全部产品的3%。在这里，97%和3%均为成数。若用N1表示具有某种标志表现的单位数，N0表示不具有这种标志表现的单位数，N表示总体单位数，则成数可写为：

式中，p和q分别表示具有或不具有某种标志的成数。

同一总体两种成数之和等于1。用公式表示为：

p＋q＝1或q＝1－p

（二）是非标志的平均数

是非标志表现了现象质的差别，因此，计算其平均数首先要将是非标志的两种表现进行量化处理，用“1”表示具有某种表现，用“0”表示不具有某种表现。

在前面的例子中，以“1”代表合格，以“0”代表不合格，然后以“1”和“0”作为变量值，计算其加权算术平均数。其公式为：

【例4－30】仍用前面的例子来说明是非标志的平均数的计算方法，见表4－18所示。(www.daowen.com)

可以看出，是非标志的平均数即为被研究标志表现的成数（此例为合格产品占全部产品的比重，即合格率）。

表4－18　计算表

（三）是非标志的标准差

根据前面所述标准差的计算方法，是非标志的标准差是将变量值“1”“0”分别减去其平均数“p”的离差平方的平均数再开平方。即：

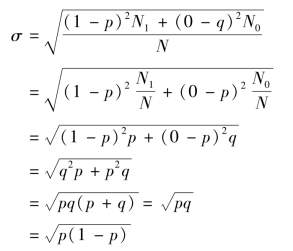
由此可见，是非标志的标准差为被研究的标志表现的成数p与另一种表现的成数（1－p）乘积的平方根。

其方差σ2为：

前面的例子已计算出合格品的成数（即合格率）是97%，其标准差为：

很容易证明，当p＝q＝0．5时，是非标志的标准差和方差达到最大可能值0．25和0．5，当p＝0或q＝0时，该标志的方差和标准差达到最小可能值0。