算术平均数、众数、中位数三者在数量上的关系决定于分配数列的分布情况。

在正态分布的情况下，标志值的分布以算术平均数为中心，两边对称分配，离中心越远的标志值次数越少，愈靠近中心的标志值次数越多，形成钟形分布，这时中位数、众数和算术平均数完全相等。

在偏态分布情况下，即由于总体出现特大或特小的极端标志值使分布曲线不再是对称的情况下，极端标志值对于众数、中位数和算术平均数的影响是不同的，众数不受极端值的影响，中位数只受极端值所引起的中间位置变动的影响，而不受标志值大小的影响，极端值对算术平均数影响最大。因此当有特大的标志值出现时，算术平均数向右远离众数，中位数次之，如图4－1所示。有下列不等式关系：

这种分布的偏斜称为右偏斜或正偏斜。

当有特小的标志值出现时，也是算术平均数最敏感：向左远离众数，中位数次之，如图4－2所示。有下列不等式关系：

这种分布的偏斜称为左偏斜或负偏斜。

不论何种偏斜，中位数总是在众数和算术平均数之间，经验表明，在适度偏斜的情况下，众数与中位数的距离约为中位数与算术平均数距离的2倍。即：

由可得：

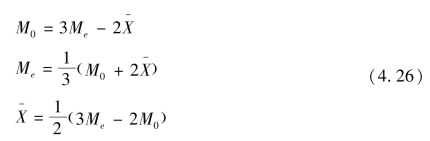(www.daowen.com)

如果知道其中两个数，就可以利用上述关系式近似地估计第三个数，并判断其偏态方向。

【例4－21】某企业工人月收入2500元的人数最多，平均收入为2900元，则月收入的中位数近似值是：

其关系为，表明是右偏分布。

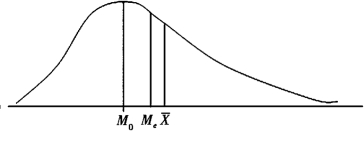
图4－1　右偏分布

又如，某高校学生的月消费额50%以上的大于850元，经测试出现最多为950元，可以估计月消费额的算术平均数为：

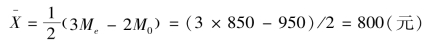
其关系为表明是左偏分布。

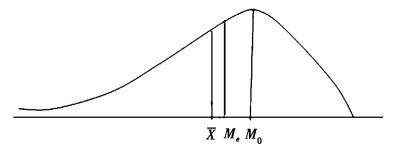
图4－2　左偏分布