编制变量分配数列，主要目的是要反映总体的分布特征，并进一步研究总体的构成及变化规律等，而频数和频率是反映数列分布特征的。因此，变量数列编制的好与坏，关键要看其能否反映总体的分布特征，即要看各组频数与频率的分配是否符合客观规律。

变量数列的编制是较为复杂的。下面以一个实例来说明变量数列的编制方法。

【例3－2】根据下面的资料编制变量数列。

某班40名同学某次数学成绩调查资料为：

68　72　84　56　70　51　86　93　95　73　78　82　87　86　64　75　78　74　74　77　85　82　63　74　79　80　97　78　92　71　71　84　86　75　76　68　75 76　82　66

这些数据资料是比较凌乱的，不能直接反映总体的特征，因此，我们需要对之加以整理，形成分配数列，以反映总体的分布特征。

首先，将原始资料按数值大小排列，确定变量值的变动范围。

51　56　63　64　66　68　68　70　71　71　71　72　73　74　74　74　75　75　75　76　76　77　78　78　78　79　80　82　82　82　84　84　85　86　86　86　87　90　93　95　97(www.daowen.com)

通过这样的排序，我们可以得到这样一个基本认识：40名同学的学习成绩并不是杂乱无章的，而是呈现出一定的规律性的：第一是其波动范围在51分至97分之间，差距为46分；第二是可以看出学习成绩大多数在70分至90分之间，偏低或者偏高的都好少。

其次，确定组数和组距。由于学生成绩的变动幅度较大，如果采用单项式分组，则组数过多，不足以反映总体中不同性质组成部分的分布特征，因此可以考虑用组距式分组，组数的确定要根据研究现象的具体情况而定。对于学习成绩的分析主要从不及格、及格、中等、良好以及优秀方面来考虑。这样可以将其分成五组。

组数确定后，再确定组距以及组限。成绩虽然是连续型变量。但习惯上用离散型变量的表示方法，即采用整数作为组限，并且采用重叠组限的形式。确定组限时，要注意，最低组的下限要小于或者等于最小变量值，最高组的上限应大于最大变量值。

最后，根据确定的组数、组距与组限，可将40名同学的学习成绩编制成分配数列，见表3－18所示。

表3－18　某班40名同学的数学成绩分配数列

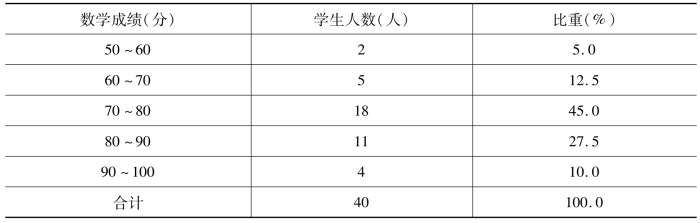
从表3－18这个分配数列中，我们可以看出，这40名同学的学习成绩是“两头小，中间大”的分布，是符合学生学习成绩这一变化规律的，反映了总体的分布特征。