根据分组标志的种类不同，统计分组方法有品质标志分组方法和数量标志分组方法之分。

（一）品质标志分组法

品质标志分组法就是选择反映事物属性差异的品质标志为分组标志，并在品质标志的变异范围内划定各组界限，将总体划分为若干个性质不同的组成部分。按品质标志分组，分组标志一经确定，组数的多少与各组之间的界限就是明确而稳定的。例如，人口总体按性别可分为男和女两组，研究国民经济总体时，可以通过按经济类型、隶属关系、地区、国民经济产业部门等品质标志分组。如表3－7所示。

表3－7　我国2012年GDP及其构成

资料来源：《中国统计摘要（2012）》

（二）数量标志分组法

数量标志分组法就是按选择反映事物数量差异的数量标志为分组标志，并在数量标志的变异范围内划定各组界限，将总体划分为性质不同的若干组成部分，如企业按固定资产价值分组、企业按职工人数分组、学生按考试分数分组、人口按年龄分组等。

社会经济现象的特征是通过数量表现出来的；针对每一个个别事物来讲，在一定时间上其数量表现是不变的，并且在按照数量标志对现象分组后的各组界限也是固定的。因此，分组后进行归类的结果也是固定的，即在按数量标志进行分组时，对于所选择的数量标志和各组的数量界限的确定上不会发生理解上的差异。这种分组方法在统计中是比较好运用的。

同时，我们明确指出应注意以下两个问题。首先，按数量标志分组的目的并不是单纯确定各组在数量上的差别，而是要通过数量上的变化来区别各组的不同类型和性质。例如，学生按学习成绩分组时就不能把55分和64分合在一组，因为这样的分组没有区分及格和不及格这两者质的区别；其次，采用最恰当的分组形式，即究竟以什么数量作为划分标准，总共可以划分为多少个组，各组之间的临界值是怎么确定的。这个问题比较复杂，我们分以下方面来探讨：

1.单项式分组和组距式分组

单项式分组是指依次将每一个数量标志值（变量值）作为一个组，适合于离散型变量且变量值变动幅度较小的场合。如对某市100个家庭按拥有住房的套数分组：0个、1个、2个、3个等（见表3－8）。

表3－8　某市100个家庭按房屋套数分组

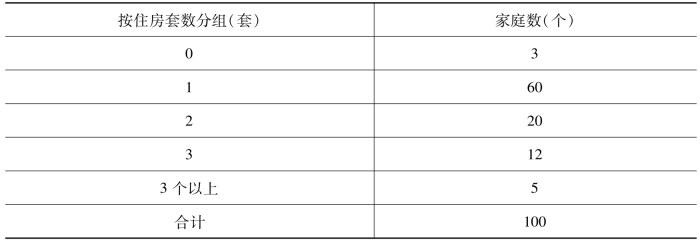
上面的“0个”“1个”“2个”……就是单项式分组的组名称，具有离散型的数量特征。

组距式分组就是将数量标志值（变量值）划分为几段区间，各值相对应于一个区间即一个组，区间的距离就是组距，所以才叫这样的分组方法为组距式分组。在某些场合，如果离散型变量值变动很大，项数又很多，如采用上述的单项式分组，那么分组数会很多，每组也占不到几个单位，这样就失去了分组的意义。例如，将我国所有企业按职工人数进行分组，由于各企业职工人数差别很大，企业职工人数相同的概率是很小的。因此对变动范围较大的离散型变量，适宜采用组距式分组。而连续型变量由于不能一一列举它的变量值，不能作为单项式分布，只能进行组距式分组。例如，某城市1000位居民按月收入分组，可做成如下组距式分组（见表3－9）。

表3－9　按居民月收入的组距式分组表(www.daowen.com)

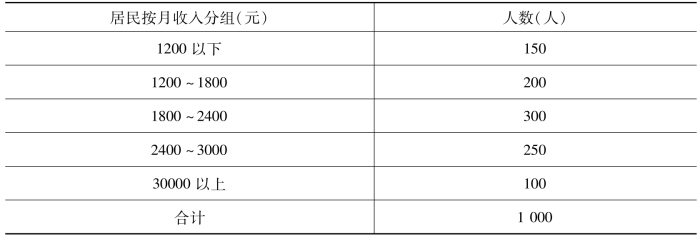
需要指明的是，按组距式分组会使资料的真实性受到一些损害。假定上例中人均月收入水平1800～2400元有300人，这300人的实际月收入可能情况是：大多数人的实际月收入可能靠近1800元，也可能靠近2400元，可均匀分布于1800～2400元之间。所有这些情况都被抽象了、忽略了。在实际研究中，只好假定是均匀分布的，这显然不符合实际。

通过组距式分组，把各组内部各单位的次要差异抽象了，而把各组之间的主要差异突出来，这样，各组分配的规律性可以更容易显示出来。根据这个道理，如组距太小，分组过细，容易将属于同类的单位划分到不同的组，因而显示不出现象类型的特点；但如果组距太大，组数太少，会把不同性质的单位归并到同一组中，失去区分事物的界限，达不到正确反映客观事实的目的。因此，组距的大小、组数的确定应根据研究对象的经济内容和标志值的分散程度等因素，不可强求一致。

2.等距分组和异距分组

等距分组是各组保持相等的组距，也就是说各组标志值的变动都限于相同的范围。从原则上来说，凡是标志值分布比较均匀的场合，均可采用等距式分组。例如学生按年龄、学习成绩的分组。等距分组的好处在于：比较省事，便于计算和分析，便于绘制统计图，如表3－10所示。

表3－10　某班学生考试成绩

异距分组即各组组距不相等的分组。统计分组时采用等距分组还是异距分组，取决于研究对象的性质特点。目的主要是把性质相同的单位合并在一个组内，性质不同的单位区分开来。例如，对某县城的零售商店按年营业额的分组，各商店的年营业额差异很大，如采用等距分组，组数过多，很难表现其分布规律，可以考虑用不等距分组，如表3－11所示。

表3－11　某县城零售商店按年营业额的分组

3.组数、组限、组中值

组距的大小与组数的多少，有着十分密切的关系。组数越多，组距越小；组数越少，组距越大。在进行组距分组时，要根据研究的目的来确定组数，同时要本着能简单明了地反映问题的原则来恰当地确定组数。确定组数后，还应确定组距。在全距（最大变量值与最小变量值之差）一定的情况下，组距的大小和标志变量数列的全距大小成正向变化，与组数多少成反向变化。

组距数列中，每个组都有端点数值，这个端点数值就是组限。上端点数值或组内最大变量值为上限，下端点数值或组内最小变量值为下限。组限的表示方式取决于变量类型，连续变量分组，需采用重叠组限，即连续一个数值作为相邻两组的上下限；离散变量分组，可采用间断组限，即两个数值作为相邻两组的上下限，也可采用重叠组限形式。采用重叠组限，在向各组内分配总体单位时，应遵循“上限不在本组内，下线在本组内”的原则，遇有特殊变量值不便另行分组的，可采用开口组的形式，即用“××以上”或“××以下”表示的组。

组距式分组之后，为了反映分布在各组中个体单位变量值的一般水平，常用组中值作为各组的代表值，这样就掩盖了各组内的标志值的具体分布情况。组中值是上下限之间的中点数值，它并不是各组标志值的平均数，各组标志值的平均值在统计分组后很难计算出来，就常以组中值近似代替。组中值仅存在于组距式分组数列中，单项式分组中不存在组中值。有关闭口组的组中值通常根据各组上限、下限进行简单平均求得，公式为：

在组距分组中存在开口组的情况下，开口组的组中值的确定，一般可将邻组组距假定为开口组组距，然后计算组中值。公式为：